Oh, alright then, more chaotic than normal - OK? And what else do you expect as I, a man who failed maths, physics and chemistry exams not just by a smidgen but by a mile, attempt to write a post on the late, great Benoit B. Mandelbrot. On my wall, just above my computer screen is a framed picture of the Mandelbrot set which, apart from their scientific interest, are a beautiful set of images in their own right. It was given to me by the cast of my production of Tom Stoppard's play Arcadia, in my opinion one of the greatest plays of the 20th century, and I treasure it not just for the beauty of the images and the pleasant memories of a production I was proud to be associated with, but also for constant reminder of what a brilliant observer and thinker Mandelbrot was.
Take a look at a cauliflower - go on, try it! - and you will see that it has a rough floral form.

Additional: Courtesy of 'SoD', see Comment below, here is a Roumanian cauliflower which is obviously off its head on fractals!

When you look closer you will see that the 'head' of the cauliflower is made up of lots of smaller 'cauliflowers', or florets as they are called. Each of these florets looks almost exactly like the cauliflower itself. If you seperate one floret from the main flower and carefully pull out one of its mini-florets that, too, would look like a tiny version of the big cauliflower. If you then placed the mini-floret under a microscope and pulled out . . . and so on and on. In other words, Mandelbrot spotted that there is an underlying similarity in nature and believing that at the heart of everything in the universe lies mathematics he set about working out the mathematics of irregular but similar natural forms. This, of course, set him at odds with the High Priests of classical mathematics who were only concerned with the mathematics of regular forms. Here is a passage of dialogue from Tom Stoppard's Arcadia spoken by Thomasina, a child genius living in the early 19th century and Septimus, her intelligent and thoughtful tutor:
Thomasina: [...] Each week I plot your equations dot for dot, xs against ys in all manner of of algebraic relation, and every week they draw themselves as commonplace geometry, as if the world of forms were nothing but arcs and angles. God's truth, Septimus, if there is an equation for a curve like a bell, there must be an equation for one like a blubell, and if a bluebell, why not a rose? Do we believe nature is written in numbers?
Septimus: We do.
Thomasina: Then why do your equations only describe the shapes of manufacture?
Septimus: I do not know.
Thomasina: Armed thus, God could only make a cabinet.
Septimus: He has a mastery of equations which leads into infinities where we cannot follow.
Thomasina: What a faint-heart! We must work outward from the middle of the maze. (She picks up the apple leaf) I will plot this leaf and deduce its equation. You will be famous for being my tutor when Lord Byron is dead and forgotten.
And Stoppard is a genius, too, for encapsulating a hellishly complex scientific concept in such charming and pellucid dialogue.
Mandelbrot's observation of self-similarity at different levels was not confined to cauliflowers or even just to flora, as Jim Holt reminds us in the New York Review of Books:
Other self-similar phenomena, each with its distinctive form, include clouds,
coastlines, bolts of lightning, clusters of galaxies, the network of blood vessels in our bodies, and, quite possibly, the pattern of ups and downs in financial markets. The closer you look at a coastline, the more you find it is jagged, not smooth, and each jagged segment contains smaller, similarly jagged segments that can be described by Mandelbrot’s methods. Because of the essential roughness of self-similar forms, classical mathematics is ill-equipped to deal with them.
Mr. Holt was reviewing a memoir written by Mandelbrot shortly before his death in 2010 entitled The Fractalist: Memoir of a Scientific Maverick which has just been published. I suppose, when you think about it, it's obvious that naturally occurring things will look similar at different levels of magnification. The trouble is that we plodders never do think about it, we needs must wait for the Mandelbrots of this world to tell us 'the bleedin' obvious'! Here is a simple example of the Mandelbrot Set in which each picture is the blown up picture of the tiny square in the preceding picture:
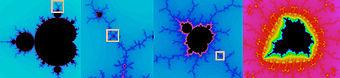

set
Here is a more extended sequence and if you look closely at each preceding picture you will be able to see the tiny detail which has been magnified:






























Yes, indeed, now cauliflowers will never seem quite the same, will they?!
(I think even Stoppard would enjoy that little witticism!)
