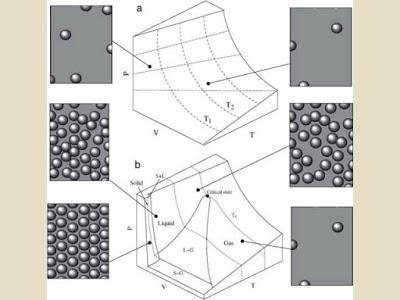
 Image: Phase diagram of water, Solé. Phase Transitions, 4
Image: Phase diagram of water, Solé. Phase Transitions, 4I've proposed to understand the concepts of emergence and generativeness as being symmetrical (link). Generative higher-level properties are those that those that can be calculated or inferred based on information about the properties and states of the micro-components. Emergent properties are properties of an ensemble that have substantially different dynamics and characteristics from those of the components. So emergent properties may seem to be non-generative properties. Further, I understand the idea of emergence in a weak and a strong sense: weakly emergent properties of an ensemble are properties that cannot be derived from the characteristics of the components given the limits of observation or computation; and strongly emergent properties are ones that cannot be derived in principle from full knowledge of the properties and states of the components. They must be understood in their own terms.
Conversations with Tarun Menon at the Tata Institute for Social Sciences in Mumbai were very helpful in allowing me to broaden somewhat the way I understand emergence in physical systems. So here I'd like to consider some additional complications for the theory of emergence coming from one specific physical finding, the mathematics of phase transitions. Complexity scientists have spent a lot of effort on understanding the properties of complex systems using a different concept, the idea of a phase transition. The transition from liquid water to steam as temperature increases is an example; the transition happens abruptly as the system approaches the critical value of the phase parameter -- 100 degrees centigrade at constant pressure of one atmosphere, in the case of liquid-gas transition.
Richard Solé presents the current state of complexity theory with respect to the phenomenon of phase transition in Phase Transitions. Here is how he characterizes the core idea:
In the previous sections we used the term critical point to describe the presence of a very narrow transition domain separating two well-defined phases, which are characterized by distinct macroscopic properties that are ultimately linked to changes in the nature of microscopic interactions among the basic units. A critical phase transition is characterized by some order parameter φ( μ) that depends on some external control parameter μ (such as temperature) that can be continuously varied. In critical transitions, φ varies continuously at μc (where it takes a zero value) but the derivatives of φ are discontinuous at criticality. For the so-called first-order transitions (such as the water-ice phase change) there is a discontinuous jump in φ at the critical point. (10)So what is the connection between "emergent phenomena" and systems that undergo phase transitions? One possible connection is this: when a system undergoes a phase transition, its micro-components get rapidly reconfigured into a qualitatively different macro-structure. And yet the components themselves are unchanged. So one might be impressed with the fact that the pre- and post-macro states correspond to very close to the same configurations of micro-states. The steaminess of the water molecules is triggered by an external parameter -- change in temperature (or possibly pressure), and their characteristics around the critical point are very similar (their mean kinetic energy is approximately equal before and after transition). The diagram above represents the physical realities of water molecules in the three phase states.
Solé and other complexity theorists see this "phase-transition" phenomenon in a wide range of systems, including simple physical systems but also biological and social systems as well. Solé offers the phenomenon of flocking as an example. We might consider whether the phenomenon of ethnic violence is a phase transition from a mixed but non-aggressive population of individuals to occasional abrupt outbursts of widespread conflict (link).
The disanalogy here is the fact that "unrest" is not a new equilibrium phase of the substrate of dispersed individuals; rather, it is an occasional abnormal state of brief duration. It is as if water sometimes spontaneously transitioned to steam and then returned to the liquid phase. Solé treats "percolation" phenomena later in the book, and rebellion seems more plausibly treated as a percolation process. Solé treats forest fire this way. But the representation works equally for any process based on contiguous contagion.
What seems to be involved here is a conclusion that is a little bit different from standard ideas about emergent phenomena. The point seems to be that for a certain class of systems, these systems have dynamic characteristics that are formal and abstract and do not require that we understand the micro mechanisms upon they rest at all. It is enough to know that system S is formally similar to a two-dimensional array of magnetized atoms (the "Ising model"); then we can infer that phase-transition behavior of the system will have specific mathematical properties. This might be summarized with the slogan, "system properties do not require derivation from micro dynamics." Or in other words: systems have properties that don't depend upon the specifics of the individual components -- a statement that is strongly parallel to but distinct from the definition of emergence mentioned above. It is distinct, because the approach leaves it entirely open that the system properties are generated by the dynamics of the components.
This idea is fundamental to Solé's analysis, when he argues that it is possible to understand phase transitions without regard to the particular micro-level mechanisms:
Although it might seem very difficult to design a microscopic model able to provide insight into how phase transitions occur, it turns out that great insight has been achieved by using extremely simplified models of reality. (10)Here is how Solé treats swarm behavior as a possible instance of phase transition.
In social insects, while colonies behave in complex ways, the capacities of individuals are relatively limited. But then, how do social insects reach such remarkable ends? The answer comes to a large extent from self-organization: insect societies share basic dynamic properties with other complex systems. (157)Intuitively the idea is that a collection of birds, ants, or bees may be in a state of random movement with respect to each other; and then as some variable changes the ensemble snaps into a coordinated "swarm" of flight or movement. Unfortunately he does not provide a mathematical example illustrating swarm behavior; the closest example he provides has to do with patterns of intense activity and slack activity over time in small to medium colonies of ants. This periodicity is related to density. Mark Millonas attempted such an account of swarming in a Santa Fe Institute paper in 1993, "Swarms, Phase Transitions, and Collective Intelligence; and a Nonequilibrium Statistical Field Theory of Swarms and Other Spatially Extended Complex Systems " (link).
This work is interesting, but I am not sure that it sheds new light on the topic of emergence per se. Fundamentally it demonstrates that the aggregation dynamics of complex systems are often non-linear and amenable to formal mathematical modeling. As a critical variable changes a qualitatively new macro-property "emerges" from the ensemble of micro-components from which it is composed. This approach is consistent with the generativity view -- the new property is generated by the interactions of the micro-components during an interval of change in critical variables. But it also maintains that systems undergoing phase transitions can be studied using a mathematical framework that abstracts from the physical properties of those micro-components. This is the point of the series of differential equation models that Solé provides. Once we have determined that a particular system has formal properties satisfying the assumptions of the DE model, we can then attempt to measure the critical parameters and derive the evolution of the system without further information about particular mechanisms at the micro-level.
