There are people who are perfectionists, there are some who are obsessively-compulsively clinically perfectionists, and I will quickly demonstrate why their basic delusion will never be accommodated at any time or place in all of the cosmos.
Firstly, consider the Platonic idea of Forms. Aristotle dealt well with this problem in the reductio ad absurdum "third man argument," which essentially gives the conclusion that the Platonic theory of Forms merely proliferates the ontological universe of discourse, of which case there would be no qualitative difference between the realm of gross matter and the realm of Platonic Forms.
Take the two-dimensional circle. A perfect object, yes? Well, 'perfect' needs to be defined. The circle is a mathematically well-defined geometric object, even though transcendental numbers (such as π) take us to conundrums of uncountable decimal-infinitudes. But if we were to accept (and there really is no choice but to accept) the transcendence of π, of which there is ample mathematical proof, we can only conclude that though we cannot intuit its transcendence in any perception-based frame of reference, we can be satisfied with the properties of the circle as mathematically valid, and sound.
I'm speaking specifically with regard to the circumference = 2πr (r =df radius) or πd (d =df diameter). Mathematically well defined? Yes. If the idea of "perfect" is "complete," then it seems that, aside from the intuitive fuzziness of π, mathematical intuitionism aside, formally speaking, the definition seems to be complete. Of course if we were to set out to prove the proof of the circle and its properties by analyzing its inherent formal logic, we'll end up in the bootstrapped world of infinite chains of reference that mathematically lead to mathematical nowhere, and that very mathematical nowhere is simply our Mind.
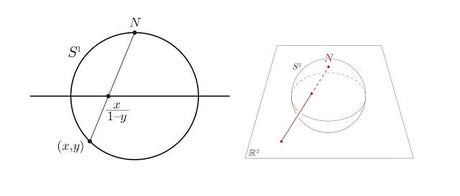
The stereographic projection of a sphere (ℝ3) onto a Cartesian two-dimensional real plane (ℝ2) presents us with a nice metaphor of this "imperfection." As the projective, bijective mapping progresses, all is well and fine until we reach the "North Pole" (0, 0, N), assuming that the "South Pole" is centered smack dab at (0, 0, 0) projected to → (0, 0). Even in this simple topological exercise, we're faced with the inevitable applicability of the Euclidean parallel axiom, viz., that the projection of point (0, 0, N) onto Cartesian 2-space ℝ2 will go off to infinity (0, ∞). So those sneaky topologists use a little sleight of hand called the "one-point compactification" of ℝ2 ∪ {(0, N)} for topological closure, and consider the matter settled. The metaphor should be self evident; even when dealing with zeros, transcendental numbers, and infinities, we come up with "holes." Ever since Bolyai, Lobachevsky, Cantor, Zeremello, and especially Gӧdel, there's no going back ever again to the Pythagorean dream world of empyrean perfection of "sacred geometry." What fills those metaphorical (and mathematical!) holes? Mind.
But let's get back to the subject at hand. So if we were to step outside the bounds of formal mathematics, we find that even the mathematical definition of the circle is an ontological castle in the sky. So let's have a look at the drawing of a circle. Take a compass and draw a circle. Is it perfect? How do you define 'perfect'? What if you were to magnify the circle drawn by, say a pencil, a hundred times? Wobbly bumps will become evident, the texture of the paper on which it is drawn, and so on, and if there is further telescoping, it will be evident that the line of the circle is a jagged, spotty mess, and fibers of the paper will appear as cavernous mountains.
What if it were drawn by laser? Consider the surface on which it is drawn; even quantum-mechanically speaking, there would be no accounting for stochastic perturbations of the surface atoms and molecules, and of the laser-drawn circumference itself, of which case the single-molecular rendering would still be subject to perturbations due to Noise, and there is no way whatsoever to "measure" its "perfect" and "complete" accuracy on a quantum level, because of Uncertainty.
So, take a look at Nature. Is Nature"perfect"? If Nature isn't "perfect," nothing would be "perfect," correct (the theological "perfection" argument is akin to that of Platonic Forms, to which the Aristotlean reductio could be reapplied)? But the fractal and Chaotic nature of Nature shows her to be very rough hewn, and there is nothing mathematically smooth about her. There is nothing about Nature that is geometrically, mathematically, compositionally, formally, structurally, symmetrically, dynamically, "perfect" in the Platonic sense of being "flawless" and "absolute" (which would assume ontological independence from everything, which is logically impossible).
So the only acceptable definition of "perfect" would be this, viz., that the adjective is synonymous to "whole" or "wholistic," which is a qualitative, quintessential idea pertaining to paradoxically interdependent self-sufficiency with nothing amiss, a nonlocal totality of interdependent, interpenetrating parts each reflecting the entirety.
Thus defined, perfection is Cosmic Wholeness, and nothing short of it will do. And inasmuch as each hologramic part, however minute, reflects the whole, everything bar none is perfect. Such being the case, you are already perfect. So anything beyond that is mere redundancy and exercise in futile delusion. Forget being a "perfectionist," you're on the wrong track; only endeavor to live in such a way that you're always mindful of your inherent Cosmic perfection.
