Learning to detect variables takes time, so our perceptual systems will only be able to become sensitive to variables that persist for long enough. The only variables that are sufficiently stable are those that can remain invariant over a transformation, and the only variables that can do this are higher order relations between simpler properties. We therefore don't learn to use the simpler properties, we learn to use the relations themselves, and these are what we call ecological information variables. (Sabrina discusses this idea in this post, where she explains why these information variables are not hidden in noise and why the noise doesn't have to be actively filtered out.)
Detecting variables is not enough, though. You then have to learn what dynamical property that kinematic variable is specifying. This is best done via action; you try to coordinate and control an action using some variable and then adapt or not as a function of how well that action works out.
While a lot of us ecological people studying learning, there was not, until recently, a more general ecological framework for talking about learning. Jacobs & Michaels (2007) proposed such a framework, and called it direct learning (go listen to this podcast by Rob Gray too). We have just had a fairly intense lab meeting about this paper and this is an attempt to note all the things we figured out as we went. In this post I will summarise the key elements, and then in a follow-up I will evaluate those elements as I try and apply this framework to some recent work I am doing on the perception of coordinated rhythmic movements.
Types of Changes to Perception and Action
J&M describe three different ways in which learning can occur- The education of intention: at any given moment I 'intend' to be engaging in one task or another. This means different information variables will be required to specify task relevant properties at different times. So what variables I am currently working with is a function of my intentions, and my intentions in a given task can change over time as I develop expertise in that task. (I would say intention is embodied in the kind of task specific device I have assembled.)
- The education of attention: for a given intention, which variable I am currently using can also vary over time. There is now a literature on the use of non-specifying variables, which in this case means 'variables that work within a small scope or to a certain degree but that are not specific to the property of interest right now'. Early learning often uses simpler but non-specifying variables and moves over time towards the specifying variable, if the system is pushed to change (e.g. see this post on work by van der Meer et al).
- Calibration: for a given intention and a given attention, there is also the need to scale the information variable in terms of action. This short-term learning process is called calibration; for example, you need to spend a little time establishing what a given optical angle means in terms of actual object size so you can grasp appropriately.
Information Spaces
The above analysis immediately points to a claim, specifically that there are multiple information variables that can support a behavior in a task. The education of attention idea is explicitly about how we switch which variable we are using. So despite the typical ecological psychology talk of 'the information variable for...', as soon as you talk about learning you have to accept the existence of multiple variables, some of which may not specify the property of interest but that might still support perception of that property in the form of functional action with respect to that property.J&M go one step further, though. Not only do they note the existence of multiple discrete informational variables in energy arrays for a given task property, they commit themselves to the idea that these variables actually live in a continuous information space, in which the variables and a set of higher order relations between those variables are all possible states of the energy array.
They give the example of a perceptual judgment task in which people are asked to estimate the peak pulling force in a stick-figure display (Experiment 4, Michaels & de Vries, 1998). In that paper, they analysed performance relative to two discrete candidate variables, maximal velocity and maximal displacement of the puller's center of mass. Here, they reanalyse the data relative to a composite variable, Eφ = cos(φ)*velocity + sin(φ)*displacement. (There are many possible higher order relations between these two variables; this equation implements one of them via addition). Then they compute the correlation with force (the dynamical property to be perceived) and all values of that equation (the x axis in Figure 1) and plot the result.
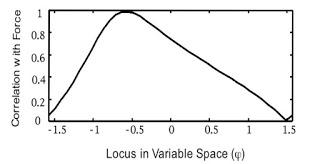
Figure 1. The information space for Eφ
Different values of this higher order relation produce different levels of performance; if you just use velocity (φ=0) then your score will top out at about 75% correct in your judgments; if you just used position (φ=1.57) then your performance would be random. Best performance is made possible by using a variable with φ~0.5.Information spaces can have more than one information dimension. In relative-mass-after-collision judgments the candidate variables are scatter angle, exit velocity, and a mass-specifying invariant. You can make them axes of a 3D information space. These higher order spaces have a problem, though; there is a redundancy in the analysis you can remove by projecting the information space down to n-1 dimensions (NOTE: I do not quite understand the reason for the redundancy). Regardless, you then do the same thing as in the 1D case; plot the correlation with each point in the information space to the dynamical property to be perceived and identify the where the best combination lives (see Figure 2).
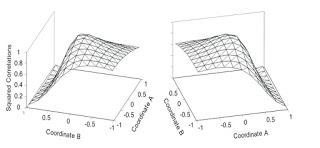
Figure 2. Two higher order information spaces with correlations to relative mass
Learning as Information Driven Motion through an Information Space
The right information space spans all the possible variables (ideally generated from a task dynamical analysis). This means that all the variables someone might use are in different parts of the space, and learning entails moving from one part of the space to another. This shows up as performance following a trajectory through different parts of the space over time. What drives and shapes this process? J&M make three assumptions.The first is that any information space is continuous, that is, you can be using a variable value from anywhere in the space (note all the pay-off functions above can be calculated throughout the space). The second is that information spaces are not flat; they have structure that is informative about errors and correcting errors. That structure is described as a vector field, with the vector direction being along the continuous surface towards the specifying invariant and the vector length being proportional to the distance. See Figure 3.
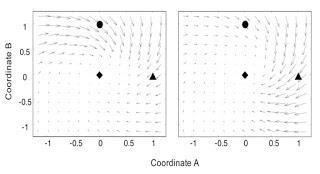
Figure 3. Information space vector fields for conditions where the invariant (diamond) always specifies the goal but the two non-specifying variables work to varying degrees.
The third assumption is worth quoting in detail (from pg 337) because it is a key claim:Most boldly, our assumption is that there exist higher-order properties of environment-actor systems that are specific to changes that reduce nonoptimalities of perception–action systems, at least in ecologically relevant environments. We also assume that there exists detectable information in ambient energy arrays that specifies such properties.We refer to this information as information for learning.Not only can you describe the information space as having this structure, this structure is a real property of the environment and there is specifying information for those properties. The idea is very ecological - how to drive a system towards a new goal if you don't want the system to have to 'know' the goal.
Summary
This is one of the first detailed ecological swings at formalising an account of the mechanism of learning. It is information based at every level, and takes no 'loans on intelligence' that plague more traditional accounts.In my next post, I will evaluate all of the central claims and assumptions of this account to see how well it holds up.

