By "mental arithmetic" I mean the ability to do arithmetic calculations rapidly and accurately 'in one's head' without benefit of paper and pencil. I'm going to quote a comment I made in a discussion over at Astral Codex Ten. The discussion was generally about Gary Marcus's criticisms of large language models. This part of the discussion was about doing arithmetic. In the third paragraph I get around to mental arithmetic:
OTOH, as a practical matter, it isn't very important that LLMs can do arithmetic well, assuming they can identify the appropriate variables in a "word problem," come up with the proper equation(s), and then pass it off to a calculation unit. However, it is interesting for diagnostic purposes since we know how people do arithmetic, assuming they do it like we were drilled in grade school.
But there's something else. I think decimal arithmetic is useful for the intuitions that can be constructed over it. What better way to get an intuition of constructing an unbounded number of objects from a small finite set? You aren't going to get that out of calculating with Roman numerals. I strongly suspect that a lot of abstract concepts rest on that kind of intuition, something David Hays and I argued here, https://www.academia.edu/243486/The_Evolution_of_Cognition.
And then there are all the "short-cut" methods that have been developed for mental calculation. Some time ago I read biographies of both Feynman and von Neumann with both mentioning how very good they were at mental calculation. In the days before hand-held calculators (and now laptops etc.) facility at mental calculation was a useful practical skill in many professions. You could buy books full of tips and tricks. People very good at it could get on TV and display their skill.
Out of curiosity I queried Google Ngrams on "mental arithmetic". We get a strong rise from about 1820 up through 1860. Then it tapers off to about 1940. Why the rise, and then the fall off, well before electronic calculators. So I checked Wikipedia on "mechanical calculator" and found this:
Thomas' arithmometer, the first commercially successful machine, was manufactured two hundred years later in 1851; it was the first mechanical calculator strong enough and reliable enough to be used daily in an office environment. For forty years the arithmometer was the only type of mechanical calculator available for sale until the industrial production of the more successful Odhner Arithmometer in 1890.
Here's the Ngram plot:
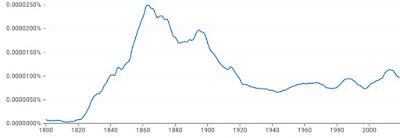
Now, I'm just guessing. The arithmometer becomes available in 1851. It takes a decade for it to become readily available. Once that happens the capacity to do mental arithmetic becomes less important. I don't know what accounts for the rise at about 1890, but that's when a new machine becomes available. In consequence, the phrase "mental arithmetic" loses salience after 1900. But what caused the in rise in 1820 and why didn't the phrase plunge after 1980 or so?

