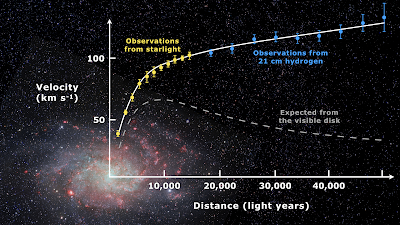
The only evidence they have for the existence of Dark Matter (Neil DeGrasse Tyson hedges his bets on this and refers to it as 'Dark Gravity') seems to be this, which I'm sure you've all seen dozens of times:
Thanks to Dinero, who reminded me a while ago about Shell Theorem, which makes doing the calculations a lot easier. I assume that the same logic applies to disk galaxies as it does to spheres, (maybe I should check with the Flat Earth Society).
So I set up the spreadsheet with approx. figures for our own galaxy (radius, thickness, number of stars), dividing it up into a center with radius 10,000 light years and nine concentric rings each 10,000 light years across (total radius 100,000 light years).
There is one variable you have to guess - by how much the density of stars goes down in each ring as you move out from the center. The output is relative speed of the stars in each ring.
Here are the results:
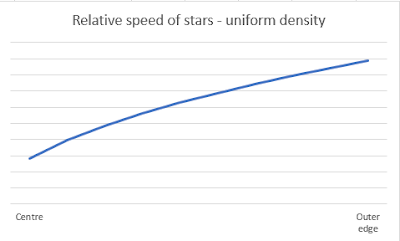
This is just a test run to illustrate that because of Shell Theorem, gravity increases and speeds increase as you go out, and is not intended to model anything real.
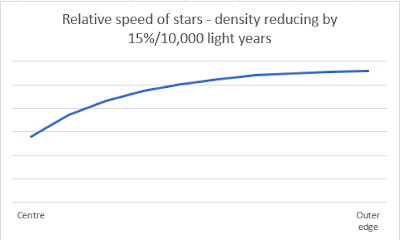
If you guess that star density goes down by 15% for each ring, you get a reasonably accurate picture of the speeds which are observed (the top curve in the first chart). The density of stars at the edge is about one-fifth of the density in the center. Because density is per unit volume, the stars at the edge would only be about twice as far apart as in the centre, which is not at all what the galaxy in the first chart looks like:
If you guess that star density goes down by 50% for each ring, you get a reasonably accurate picture of relative densities and the speed changes are what Vera Rubin et al expected to see (the bottom curve in the first chart). The density of stars at the edge is about 0.2% of the density in the center. This is a massive drop, and means that stars at the edge are about ten times as far apart as in the center (looks about right):
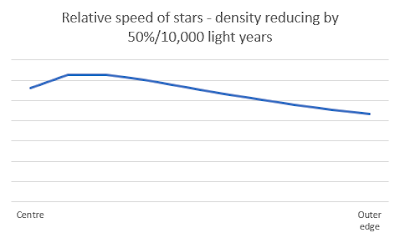
In the 15% version, you end up with about seven times as many stars in the galaxy as in the 50% version.
So, say the Dark Matterati, we can only see one-seventh of the mass we need, the rest must be Dark Matter, i.e. six units of Dark Matter for each unit of visible matter (a star). Fair enough, most people seem to accept that.
My niggle with all this is, why is there more and more Dark Matter as you go out? To get it to balance, each star in the center has no units of Dark Matter, as you go further and further out, each star has more and more units of Dark Matter, until at the outside edge, each star has about one hundred units of Dark Matter. Seems a bit convenient to me, like inventing an invisible planet to explain the precession of Mercury.
Which is why I reckon either they've simply miscounted the stars*; or it's gravitational lensing of gravity; or it's MOND; or it's whatever it is that Stacy McGaugh (Dark Matter sceptic) is trying to explain on the basis of observations of low surface brightness galaxies, the Fischer-Tully relation and so on (I don't claim to understand it, but he's very entertaining and seems very plausible).
* The problem here is, they think there are at least 100 billion stars in our galaxy, but no more than 400 billion, so the accepted most likely number is 250 billion with a huge margin of error. If you divide the volume of the galaxy by 250 billion, stars should be about 5 light years apart on average. The Sun is about one-third of the way out and is a bit less than 5 light years from the next nearest star, which seems to support the 15% version. The argument in favour of the 50% version is "just look at a galaxy!"
