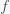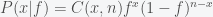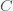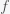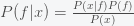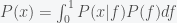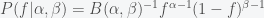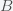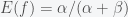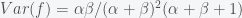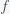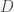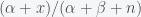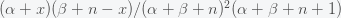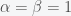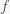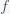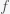Since, the discovery of exoplanets nearly 3 decades ago most astronomers, at least the public facing ones, seem to agree that it is just a matter of time before they find signs of life such as the presence of volatile gases in the atmosphere associated with life like methane or oxygen. I'm an agnostic on the existence of life outside of earth because we don't have any clue as to how easy or hard it is for life to form. To me, it is equally possible that the visible universe is teeming with life or that we are alone. We simply do not know.
But what would happen if we find life on another planet. How would that change our expected probability for life in the universe? MIT astronomer Sara Seager once made an offhand remark in a podcast that finding another planet with life would make it very likely there were many more. But is this true? Does the existence of another planet with life mean a dramatic increase in the probability of life in the universe. We can find out by doing the calculation.
Suppose you believe that the probability of life on a planet is
(i.e. fraction of planets with life) and this probability is uniform across the universe. Then if you search
planets, the probability for the number of planets with life you will find is given by a Binomial distribution. The probability that there are
planets is given by the expression
, where
is a factor (the binomial coefficient) such that the sum of
from one to
is 1. By Bayes Theorem, the posterior probability for
(yes, that would be the probability of a probability) is given by
where
. As expected, the posterior depends strongly on the prior. A convenient way to express the prior probability is to use a Beta distribution
(*)
where
is again a normalization constant (the Beta function). The mean of a beta distribution is given by
and the variance, which is a measure of uncertainty, is given by
. The posterior distribution for
after observing
planets with life out of
will be
where
is a normalization factor. This is again a Beta distribution. The Beta distribution is called the conjugate prior for the Binomial because it's form is preserved in the posterior.
Applying Bayes theorem in equation (*), we see that the mean and variance of the posterior become
and
, respectively. Now let's consider how our priors have updated. Suppose our prior was
, which gives a uniform distribution for
on the range 0 to 1. It has a mean of 1/2 and a variance of 1/12. If we find one planet with life after checking 10,000 planets then our expected
becomes 2/10002 with variance
. The observation of a single planet has greatly reduced our uncertainty and we now expect about 1 in 5000 planets to have life. Now what happens if we find no planets. Then, our expected
only drops to 1 in 10000 and the variance is about the same. So, the difference between finding a planet versus not finding a planet only halves our posterior if we had no prior bias. But suppose we are really skeptical and have a prior with
and
so our expected probability is zero with zero variance. The observation of a single planet increases our posterior to 1 in 10001 with about the same small variance. However, if we find a single planet out of much fewer observations like 100, then our expected probability for life would be even higher but with more uncertainty. In any case, Sara Seager's intuition is correct - finding a planet would be a game breaker and not finding one shouldn't really discourage us that much.