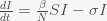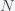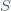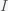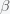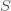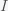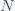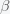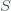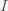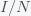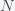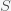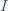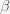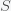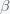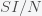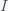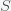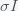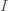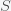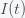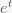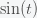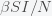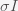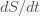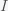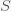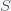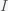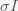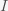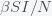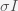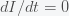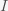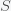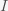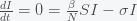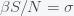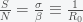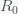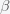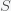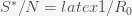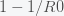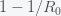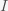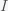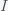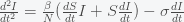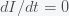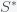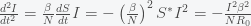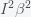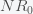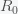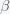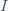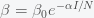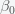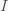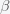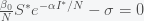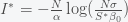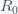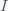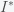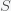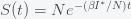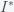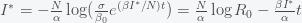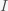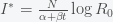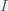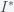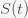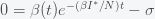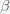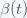For the past five weeks, the appearance rate of Covid-19 cases has plateaued at about a hundred thousand new cases per day. Just click on the Daily Cases Tab on the JHU site to see for yourself. This is quite puzzling because while individual nations and regions are rising, falling, and plateauing independently, the global total is flat as a pancake. A simple resolution to this seeming paradox was proposed by economist John Cochrane (see his post here). The solution is rather simple but the implications as I will go into more detail below are far reaching. The short answer is that if the world (either through behavior or policy) reacts to the severity of Covid-19 incrementally then a plateau will arise. When cases go up, people socially distance, and the number goes down, when cases go down, they relax a little and it goes back up again.
This can be made more precise with the now-famous SIR model. For the uninitiated, SIR stands for Susceptible Infected Recovered model. It is a simple dynamical model of disease propagation that has been in use for almost a century. The basic premise of an SIR model is that at any given time, the proportion of the population is either infected with the virus I, susceptible to infection S, or recovered from infection and no longer susceptible R. Each time an S comes across an I, it has a chance of being infected and becoming another I. An I will recover (or die) with some rate and become an R. The simplest way to implement an SIR model is to assume that people interact completely randomly and uniformly across the population and the rate of transmission and recovery is uniform as well. This is of course a gross simplification and ignores the complexity and diversity of social interactions, the mechanisms of actual viral transmission, and the progression of disease within individuals. However, even though it misses all of these nuances, it captures many of the important dynamics of epidemics. In differential equation form, the SIR model is written as

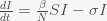
(SIR model)
where
is the total number of people in the population of interest. Here,
and
are in units of number of people. The left hand sides of these equations are derivatives with respect to time, or rates. They have dimensions or units of people per unit time, say day. From this we can infer that
and
must have units of inverse day (per day) since
,
, and
all have units of numbers of people. Thus
is the infection rate per day and
is the recovery/death rate per day. The equation assumes that the probability of an
meeting an
is
. If there was one infected person in a population of a hundred, then if you were to interact completely randomly with everyone then the chance you would run into an infected person is 1/100. Actually, it would be 1/99 but in a large population, the one becomes insignificant and you can round up. Right away, we can see a problem with this assumption. I interact regularly with perhaps a few hundred people per week or month but the chance of me meeting a person that had just come from Australia in a typical week is extremely low. Thus, it is not at all clear what we should use for
in the model. The local population, the regional population, the national population?
The model assumes that once an
has run into an
, the rate of transmission of the virus is
. The total rate of decrease of
is the product of
and
. The rate of change of
is given by the increase due to interactions with
and the decrease due to recovery/death
. These terms all have units of person per day. Once you understand the basic principles of constructing differential equations, you can model anything, which is what I like to do. For example, I modeled the temperature dynamics of my house this winter and used it to optimize my thermostat settings. In a post from a long time ago, I used it to model how best to boil water.
Given the SIR model, you can solve them to get how
and
will change in time. The SIR model is a system of nonlinear differential equations that do not have what is called a closed-form solution, meaning you can't write down that
is some nice function like
or
. However, you can solve them numerically on a computer or infer properties of the dynamics directly without actually solving them. For example, if
is initially greater than
, then $dI/dt$ is positive and thus $I$ will increase with time. On the other hand, since
is always negative (rate of change is negative), it will decrease in time. As
increases and
decreases, since
is decreasing at a faster rate than
is increasing because
is slowing the growth of
, then at some point
will equal
and
. This is a stationary point of
. However, it is only a momentary stationary point because
keeps decreasing and this will make
start to decrease too and thus this stationary point is a maximum point. In the SIR model, the stationary point is given by the condition
(Stationary condition)
which you can solve to get either
or
. The
point is not a peak but just reflects the fact that there is no epidemic if there are no infections. The other condition gives the peak:
where
is the now-famous R naught or initial reproduction number. It is the average number of people infected by a single person since
is the infection rate and
is the infection disappearance rate, the ratio is a number. The stationary condition gives the herd immunity threshold. When the fraction of
reaches
then the pandemic will begin to decline. This is usually expressed as the fraction of those infected and no longer susceptible,
. The 70% number you have heard is because
is approximately 70% for
, the presumed value for Covid-19.
A plateau in the number of new cases per day is an indication that we are at a stationary point in
. This is because only a fraction of the total infected are counted as cases and if we assume that the case detection rate is uniform across all
, then the number of new cases per day is proportional to
. Thus, a plateau in cases means we are at a stationary point in
, which we saw above only occurs at a single instance in time. One resolution to this paradox would be if the peak is broad so it looks like a plateau. We can compute how broad the peak is from the second derivative, which gives the rate of change of the rate of change. This is the curvature of the peak. Taking the second derivative of the I equation in the SIR model gives
Using
and the formula for
at the peak, the curvature is
It is negative because at a peak the slope is decreasing. (A hill is easier to climb as you round the top.) There could be an apparent plateau if the curvature is very small, which is true if
is small compared to
. However, this would also mean we are already at the herd immunity threshold, which our paper and recent anti-body surveys predict to be unlikely given what we know about
.
If a broad peak at the herd immunity threshold does not explain the plateau in new global daily cases then what does? Cochrane's theory is that
depends on
. He postulated that
,where
is the initial infectivity rate, but any decreasing function will do. When
goes up,
goes down. Cochrane attributes this to human behavior but it could also be a result of policy and government mandate. If you plug this into the stationary condition you get
or
and the effective reproduction number
is one.
However, this is still only a quasi-stationary state because if
is a constant
, then
will decrease as
, which has solution
(S)
Plugging this into the equation for
gives
which means that
is not really plateaued but is decreasing slowly as
We can establish perfect conditions for a plateau if we work backwards. Suppose again that
has plateaued at
. Then,
is given by equation (S). Substituting this into the (Stationary Condition) above then gives
or
which means that the global plateau is due to us first reducing
to near
, which halted the spread locally, and then gradually relaxing pandemic mitigation measures so that
is creeping upwards back to it's original value.
The Covid-19 plateau is both good news and bad news. It is good news because we are not seeing exponential growth of the pandemic. Globally, it is more or less contained. The bad news is that by increasing at a rate of a hundred thousand cases per day, it will take a long time before we reach herd immunity. If we make the naive assumption that we won't reach herd immunity until 5 billion people are infected then this pandemic could blunder along for
days! In other words, the pandemic will keep circling the world forever since over that time span, babies will be born and grow up. Most likely, it will become less virulent and will just join the panoply of diseases we currently live with like the various varieties of the common cold (which are also corona viruses) and the flu.