My daughter knows the relative side lengths of 45-45-90 and 30-60-90 triangles (they are right angle triangles because there's a 90) off by heart (she needs them for maths competitions) and laughs at me when I forget them.
I stumbled across the 15-75-90 triangle by accident a couple of weeks ago and it had fairly easy-to-remember side lengths. But I couldn't remember what they were, how I did it or find my scribbled workings, so I Binged it (this is like 'Googling' something, but using Bing) and found an explanation at Robert Loves Pi.
That all seems a bit long-winded to me, so here is the shorter version:
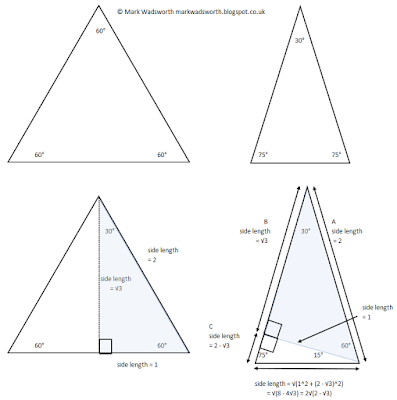
1. Draw an equilateral triangle.
2. Draw an isosceles triangle with interior angles 30-75-75.
3. Divide the equilateral triangle vertically to give you a 30-60-90 triangle. The (relative) side lengths of the base and hypotenuse are 1 and 2, so the vertical is √3. Colour this pale blue.
4. Put the pale blue 30-60-90 triangle on top of the isosceles triangle. Then do the numbers. The angle at the bottom left is still 75°. The angle at the bottom right is 75° - 60° = 15°. The base of the smaller triangle (side C) is 2-√3 (i.e. side A minus side B) and the other known side is 1. Add the squares of those two and take the square root of the answer, which simplifies down to 2√(2- √3)*.
Click to enlarge:
* Jason Tyler in the comments at Robert Loves Pi says "If you don’t like nested radicals, you can express 2√(2-√3) as √6 – √2"
How did he do this?
Start again with the sum of the squares of 1 and 2-√3
= 8 - 4√3.
= 6 - 4√3 + 2
= 6 - 2√12 + 2
Remember that √12 = √6 x √2...
= (√6 - √2)(√6 - √2)
so the square root of '8 - 4√3' = √6 - √2.
This is a neat trick, but only seems to work in some circumstances, where you can put the first expression into the form 'A - 2√AB + B'.
