Sewall Wright lived to be 98. Two months before he died he published a paper in The American Naturalist titled Surfaces of Selective Value Revisited (Wright, 1988).Wright was interested in adaptive evolution, and he originated the concept of fitness landscapes to qualitatively describe differences in fitness without using mathematics. He first called them adaptive landscapes, but also used surfaces of selective value.
Today we mostly call them fitness landscapes, though they were initially termed adaptive landscapes.
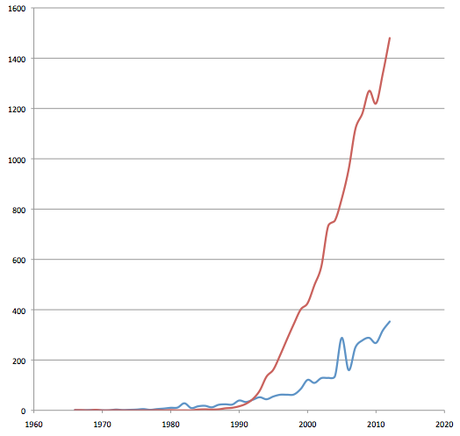As you can see from this figure that I made using data from Google Scholar, in most papers nowadays people refer to them as 'fitness landscapes' (red line) vs. 'adaptive landscapes'. I obtained this data by searching for either term in Google Scholar by year.Evidently, the idea of fitness landscapes is catching on, to say the least. A Google Scholar search I just did returned well over 2,000 articles that used one of the terms in 2013. The reason for the wide usage is that the concept is very powerful and intuitive. Once the structure of the fitness landscape is known to some extent, we can understand evolutionary dynamics, i.e., how populations evolve can be predicted. I have written about that before (
Smooth and rugged fitness landscapes, Can we predict evolution?, Crossing valleys in fitness landscapes), and have recently put up a number of movies that visualize the processI view fitness landscapes as being an explanatory framework similar to that of phylogenetic trees. These familiar trees are how we visualize the evolutionary past, and in the same way thinking about evolution forward in time I suggest is best done with fitness landscapes.
Basically, a fitness landscape is just something that describes fitness as a function of either the phenotype (the traits) or the genotype (the genes) of an organism (few people seem to have much use of the type of fitness landscapes where fitness is a function of allele frequencies, so I'll ignore it here, as I generally do). The problem is then how to visualize this map, and when there are only two dimensions, for example when there are only two traits (when we are ignoring all other traits), then the fitness landscape can be depicted as a two-dimensional surface where the height is fitness and depends on the two trait-values. You can see examples of populations evolving on such landscapes in the movies I referred to above.Sewall Wright drew the first fitness landscape like this. It is originally from his 1932 paper, but was reused in the 1988 paper.
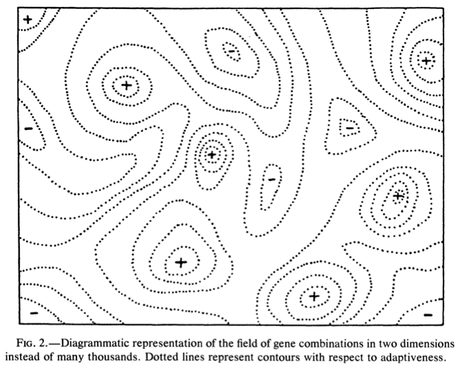
Unfortunately, this kind of map has since come under attack for being simplistic, misleading, and wrong. The main criticism is that real fitness landscapes are multi-dimensional, with many different traits (or many different loci/genes/nucleotides, in the case of a genotype-fitness landscape) making it impossible to visualize the whole thing in its entirety on a piece paper in a book. Thus, fitness landscapes has gotten flak for boiling the truth down to two dimensions, which then misleads the reader into thinking they can get an intuitive feeling for evolution when they really do not.
One such serious criticism was raised by Sergey Gavrilets who (long after Wright's death) gave a mathematical argument that multi-dimensional landscape will have neutral ridges (paths with no change in fitness) between any pair of genotypes, and population can therefore always evolve by neutral evolution, and crossing valleys in the fitness landscape is therefore not necessary (Gavrilet and Gravner, 1997). Valley-crossing is a famous problem in evolutionary biology, but it has been shown that populations can cross valleys routinely (Weissman et al., 2009; Østman et al., 2012), but never mind that for now. So, something profound supposedly happens when the dimensionality goes from two to very large that changes the structure of the landscape so fundamentally that the intuitions that we get from looking at two-dimensional maps do not transfer to higher dimensions.
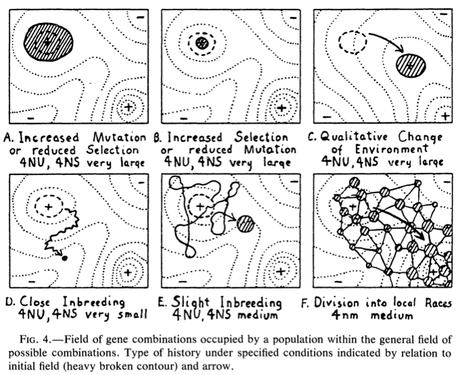
Wright's last paper was, I have heard, supposed to address the shortcomings of the fitness landscape "metaphor" (not sure if that word was used back then, but it was later used by Kaplan and by Pigliucci who both denounces fitness landscapes following Gavrilets). However, finally coming to the point of what I wanted to say, I have now read that 1988 paper, and as far as I can see, Wright does nothing to discourage the use of fitness landscapes. The first five pages out of eight is spent describing fitness landscapes. In addition to his figure 2 above, he also reuses figures 3 and 4, the latter of which you can see here describing how a population can move through a rugged (i.e., multi-peaked) fitness landscape, including figure 4F, where the population moves from the original, sub-optimal peak in the upper left to the higher peak in the lower right via Wright's own proposed process of Shifting Balance (which involves genetically drift in geographically separated subpopulations and migration between them).
Wright then says this on the sixth page:
I became some-what dissatisfied with the substitution of a two-dimensional surface of selective values for the true pattern, which is multidimensional both among and within loci. I decided that this pattern should be explicitly assumed to underlie the two-dimensional one of the diagram and that its origin should be at whatever peak was under consideration. The contours should be considered as merely symbolic of the complex pattern to a greater extent that before. However, I did not arrive at any changes that should be made in the diagrams as presented.This seems to me not to recant anything about the utility of fitness landscapes (aka surface of selective values), apart from admitting that two-dimensional landscapes are symbolic of the multi-dimensional nature of them.
At the end of the day, the possibility that there is something fundamentally different between fitness landscapes of low and high dimensions remain an empirical question. Fortunately, two-dimensional diagrams are not the only way the structure of fitness landscapes can be explored (see, e.g., Østman et al., 2010), and, thankfully, experimentalists are getting better and better at measuring large biological fitness landscapes. If it turns our that increasing the number of dimensions retains the multi-peaked picture as depicted above, then I rest my case. Except of course that it is always possible to argue that going from 2 to 20 to 2,000 dimensions is still not enough.
References
Gavrilets S and Gravner J (1997). Percolation on the fitness hypercube and the evolution of reproductive isolation. Journal of theoretical biology, 184 (1), 51-64 PMID: 9039400
Weissman DB, Desai MM, Fisher DS, Feldman MW (2009). The rate at which asexual populations cross fitness valleys. Theoretical population biology, 75 (4), 286-300 PMID: 19285994
Wright S (1988). Surfaces of Selective Value Revisited The American Naturalist, 131(1), pp. 115-123, DOI: 10.1086/284777
Wright S (1931). Evolution in Mendelian populations Genetics (16), pp. 97–159
Wright S (1982). The shifting balance theory and macroevolution. Annual review of genetics, 16, 1-19 PMID: 6760797
Østman B, Hintze A, and Adami C (2010). Critical properties of complex fitness landscapes Proc. 12th Intern. Conf. on Artificial Life, H. Fellerman et al., eds. (MIT Press, 2010), pp. 126-132 arXiv: 1006.2908v1
Østman B, Hintze A, and Adami C (2012). Impact of epistasis and pleiotropy on evolutionary adaptation. Proceedings. Biological sciences / The Royal Society, 279 (1727), 247-56 PMID: 21697174
