Rextinct: a New Tool to Estimate When a Species Went Extinct

If several fossils of an extinct population or species are dated, we can estimate how long ago the extinction event took place. In our new paper, we describe CRIWM, a new method to estimate extinction time using times series of fossils whose ages have been measured by radiocarbon dating. And yes, there’s an R package — Rextinct — to go with that!

While the Earth seems to gather all the conditions for life to thrive, over 99.9% of all species that ever lived are extinct today. From a distance, pristine landscapes might look similar today and millennia ago: blue seas with rocky and sandy coasts and grasslands and mountain ranges watered by rivers and lakes and covered in grass, bush and trees.

But zooming in, the picture is quite different because species identities have never stopped changing — with ‘old’ species being slowly replaced by ‘new’ ones. Fortunately, much like the collection of books in the library summarises the history of literature, the fossilised remnants of extinct organisms represent an archive of the kinds of creatures that have ever lived. This fossil record can be used to determine when and why species disappear. In that context, measuring the age of fossils is a useful task for studying the history of biodiversity and its connections to the planet’s present.

In our new paper published in the journal Quaternary Geochronology (1), we describe CRIWM (calibration-resampled inverse-weighted McInerny), a statistical method to estimate extinction time using times series of fossils that have been dated using radiocarbon dating.

Why radiocarbon dating? Easy. It is the most accurate and precise chronometric method to date fossils younger than 50,000 to 55,000 years old (2, 3). This period covers the Holocene (last 11,700 years or so), and the last stretch of the late Pleistocene (~ 130,000 years ago to the Holocene), a crucial window of time witnessing the demise of Quaternary megafauna at a planetary scale (4) (see videos here, here and here), and the global spread of anatomically modern humans (us) ‘out of Africa’ (see here and here).

Why do we need a statistical method? Fossilisation (the process of body remains being preserved in the rock record) is rare and finding a fossil is so improbable that we need maths to control for the incompleteness of the fossil record and how this fossil record relates to the period of survival of an extinct species.

A brief introduction to radiocarbon dating

First, let’s revise the basics of radiocarbon dating (also explained here and here). This chronometric technique measures the age of carbon-rich organic materials — from shells and bones to the plant and animal components used to write an ancient Koran, make a wine vintage and paint La Mona Lisa and Neanderthal caves. 

Radiocarbon dating takes advantage of the fact that carbon (the 6^th element in the periodic table known as ‘Carbon-12’ because of its atomic mass of 6 protons + 6 neutrons, and the 4^th most abundant element in the Milky Way after hydrogen, helium, and oxygen] has an isotope mass of 14 (6 protons + 8 neutrons) — this is known as ‘radiocarbon’ (often abbreviated ‘Carbon-14’, ‘¹⁴C’, or ‘C14’).

¹⁴C forms in the atmosphere as nitrogen atoms (7 protons + 7 neutrons) are bombarded by ultrafast neutrons from outer space (cosmic rays), turning 1 proton into a neutron. ¹⁴C then moves into food webs through (autotrophic) organisms, like plants and corals, that produce their own food using light, water, and carbon among other chemicals. 

During its lifetime, the ¹⁴C content of a living organism keeps constant (¹⁴C losses = ¹⁴C gains) but, right after death, ¹⁴C decays without replenishment back into nitrogen at a known rate (roughly 50% of ¹⁴C turns into nitrogen every 5,700 years). This is how fossils become molecular clocks because their ¹⁴C concentration is indicative of their age, and this clock became the basis of radiocarbon dating — a 1950s’ Nobel-prize-winning discovery awarded to chemistry professor Willard Libby.

Radiocarbon dating can be used to date fossils up to 55,000 years before present (Present = 1950). Beyond, ¹⁴C content is too low for detection by the last generation of accelerator mass spectrometry (accelerator mass spectrometers count (sub)atomic particles), the most popular technology used for radiocarbon dating today.

CRIWM properties

CRIWM assumes that the fossil record of an extinct species is incomplete, and gauges the chances of finding the fossil of the last surviving individual given the series of fossils that are known and have been radiocarbon-dated. As such, CRIWM unites the following two properties: 

• Fossil bias: The fossil record of an extinct species is scattered in space and time because the degree of preservation and fossilisation of body remains varies across the home range and period of survival of the species in question. Determining the date of extinction is tricky because the youngest known fossil might simply represent where fossils are best preserved and/or most detectable, so is unlikely to belong to the last surviving individual of an extinct population or species — a phenomenon the famous palaeontologist David Raup named the “Signor-Lipps effect” (5) honouring the first conceptualisation by his peers Philip Signor and Jere Lipps (6). 
• Dating uncertainty: Radiocarbon dating consists of first measuring the amount of ¹⁴C in a fossil and second, asking what the age of the fossil is relative to the age of a reference material of known age that has the same amount of ¹⁴C. This is called ‘calibration’ (see here and here) and, in practice, means converting the ¹⁴C years of a fossil into a real-time scale in ‘calendar years’. The reference materials used to build a calibration curve are tree rings, speleothems, corals and lacustrine/marine sediments because they grow in periodic layers that can be dated accurately and precisely. The nuance is that, despite ¹⁴C content of a fossil decreasing over time, the incorporation of ¹⁴C into food webs is not exactly linear (7-9), so two layers of different ages in a reference material might have the same ¹⁴C content. For this reason, calibration turns the ¹⁴C years of a fossil into a probability representing how probable it is that a fossil is a number of calendar years old given the temporal variability in the ¹⁴C content of the reference material. 

How CRIWM works?

Our CRIWM method adds a new tool to the battery of statistical techniques designed to estimate extinction time while controlling for the Signor-Lipps effect (10, 11). Most importantly, CRIWM becomes the first non-Bayesian approach to estimate extinction time while controlling for the uncertainty of translating ¹⁴C years into calendar years. This approach considers three aspects: (i) a definition of extinction time, (ii) a characterisation of the errors of counting ¹⁴C isotopes in a fossil, and (iii) the calculation of extinction time given the definition of extinction time and those dating errors.

• Extinction time: CRIWM is an extension of its sister method GRIWM (12). Both define extinction time as the year in which the probability of finding a fossil younger than the youngest known fossil is ‘low’. How low? The investigator fixes this threshold, which [being a probability] can range from 0 (no chance of finding a younger fossil) to 1 (100% chance of finding a younger fossil). The maths of this calculation are described in our paper (1), but scientists conservatively choose a probability threshold < 1%.
• Radiocarbon errors: Like with any measurement (e.g., the weight of a bunch of bananas or the height of a tree), ¹⁴C measurements in a study fossil come with an error. The particularity is that the error in ¹⁴C years obtained from accelerator mass spectrometry is always a bell-shaped (Gaussian or Normal) probability distribution that can be exactly characterised with its mean and standard deviation. Yet the calibration of a ¹⁴C age into calendar years becomes a probability distribution that can vary from bell-shaped to non-Normal and often highly bumpy with several ‘bells’. This occurs because the shape of the calibrated probability distribution depends on the linearity of the calibration curve at the temporal point around the ¹⁴C years measured in the study fossil. See animation here where vertical axis = age ± error in ¹⁴C years versus horizontal axis = age ± error in calendar years, blue line = calibration curve, purple contour = calibrated probability distribution.

There are calibration curves specifically tailored to calibrate ¹⁴C ages from fossils collected in different parts of the world that account for geographical differences in ¹⁴C concentrations. The most popular (and complete) calibration curves are the IntCal (13) and SHCal (14) series (IntCal04, IntCal09, IntCal13, IntCal20 / SHCal04, SHCal13, SHCal20) for terrestrial fossils from the Northern and the Southern Hemispheres, respectively, along with the Marine series (Marine13, Marine20) for marine fossils (15).

•  Calculation of extinction time: The original GRIWM approach (12) assumes that all ¹⁴C ages in a time series (representing the fossil record of extinct species) are in calendar years and each age has a normal error. GRIWM then runs in three steps: 

ONE: randomly sampling 1 value from the normal distribution of each fossil age resulting in a time series of resampled ages.

TWO: calculating extinction time as the year in which the probability of finding a new fossil (younger than the youngest known fossil) is 0.05 for the resampled time series.

THREE: repeating steps ONE and TWO 10,000 times, resulting in 10,000 estimates of extinction time from extinction time estimate 1 to extinction time estimate 10,000. Extinction time ultimately equals the median and 95% range of those 10,000 values (16).

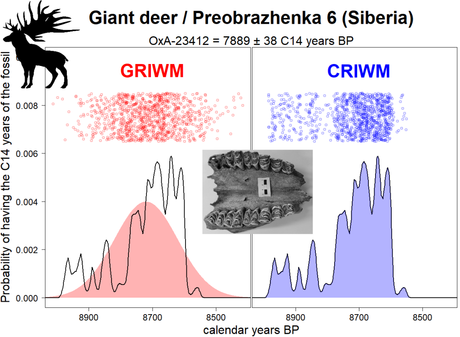
However, we show (1) that IntCal20 and SHCal20 calibrated ¹⁴C ages rarely have Normal properties; in fact, their statistical distributions often show 2 to 10 peaks that make GRIWM unrealistic for ¹⁴C chronologies. To abate this problem, the new method CRIWM assumes that all fossil ages in a time series are in ¹⁴C years and takes the preliminary step ZERO of calculating the exact calibrated probability distribution of each age. CRIWM then runs GRIWM’s steps ONE to THREE with the distinction that the random sampling (step ONE) is applied to the exact calibrated probability distribution of each age (whatever its shape). In the figure below, we show how resampling differs for CRIWM versus GRIWM for a radiocarbon date from a giant deer Megaloceros giganteus, a magnificent exponent of the Eurasian late-Quaternary megafauna (see bio-information about this extinct species here and here).

Re-sampling differences between CRIWM and GRWIM illustrated for the radiocarbon age OxA-23412 = 8712 ± 91 C14 years before present measured on a maxilla of a giant deer (Megaloceros giganteus) from Siberia. The curve (black) shows the exact probability distribution of the age (vertical axis) on a real-time scale (horizontal axis) following calibration with the IntCal20 curve. Upper dots represent 1000 calendar ages resampled from the calibrated probability distribution assumed by each method, namely Normal (GRIWM = red contour) and true (CRIWM = blue contour). In GRIWM, the closer a value is to the (theoretical) Normal mean, the more likely this value will be resampled, whereas in CRIWM the closer a value is to one of the modes of the true distribution, and the higher that mode is, the more likely that that value will be resampled. CRIWM (1) and GRIWM (12, 16) resample each age in a time series of fossils and use those resampled values to estimate extinction time . Bone image shown with permission of Yaroslav Kuzmin.

---

Other developments we made (1) that we do not describe in detail here are:

• a novel estimator of extinction time (for both CRIWM and GRIWM), which does not depend on arbtirary probability thresholds;
• the two estimators (with and without probability thresholds) can be applied to estimate extinction time, as well as arrival time if one is interested in measuring the chances of finding a fossil older than the oldest known fossil — the latter is a proxy for when a population or species should have first arrived in a given locality;
• CRIWM can handle time series of fossils including only ¹⁴C ages, or combinations of fossil ages measured by radiocarbon dating and other chronometric techniques.

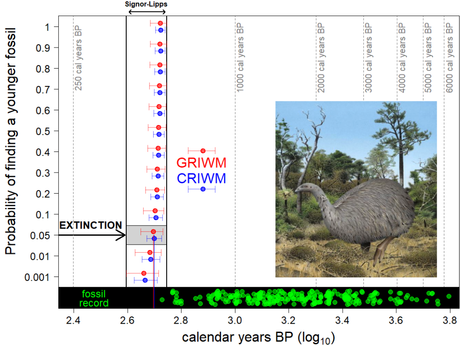
An example from Aotearoa-New Zealand — the moa

The idea of our study came along from Richard Holdaway’s work on the extinction of the moa, the giant (up to > 200 kg), flightless birds (20) surviving well into the 20^th Century after a long history of evolution, diversification, and endemism in Aotearoa-New Zealand. Holdaway and collaborators (21) justified the use of complex Bayesian stats (rather than GRIWM) to estimate the timing of extinction of moas by pointing out the unrealistic assumption of Normally distributed errors in ¹⁴C chronologies (see above).

Holdaway and colleagues’ (21) Bayesian approach resulted in the moa extinction time of 524 [554, 470] calendar years before present using SHCal13 calibrations of 270 radiocarbon-dated moa specimens collected on the South Island — ¹⁴C ages varied from 564 to 5503 years before present per fossil. We ‘criwmed’ the same dataset with SHCal13 resulting in an extinction time of 501 [533, 471] calendar years before present. Our estimate is only two decades younger and has a smaller error (i.e., narrower confidence interval) than the Bayesian estimate (1). For the same dataset, CRIWM’s moa extinction time with the most recent calibration curve SHCal20 is 497 [539, 446] calendar years before present. 

Extinction of the moa (1). Blue and red dots with segments represent CRIWM and GRIWM estimates of extinction time (estimate ± confidence interval), respectively. Shown are probabilities of finding a fossil younger than the youngest known fossil from 0.001 to 1 (vertical axis), capturing the Signor-Lipps effect in log-scaled calendar years (horizontal axis). Logically, the closer we get to the present, the lower the chances of finding the youngest-ever fossil. Both methods assign probability = 0.05 to extinction time. Across probabilities, CRIWM is consistently more precise (narrower confidence intervals) than GRIWM. The study fossil record (green circles) comprises radiocarbon ages (SHCal20 calibrations) from 268 bones and 2 coprolites (21) collected on the South Island and belonging to seven moa species (bush moa Anomalopteryx didiformis, South Island giant moa Dinornis robustus, eastern moa Emeus crassus, stout-legged moa Euryapteryx curtus, upland moa Megalapteryx didinus, crested moa Pachyornis australis, heavy-footed moa Pachyornis elephantopus). The drawing shows an eastern moa created by Paul Martinson. See video-stories about these birds here and here.

---

CRIWM available in R

We have created the R package Rextinct to run CRIWM (function = criwm) and GRIWM (function = griwm) and calibrate ¹⁴C years (function calendar) — how Rextinct works is explained in Appendix A of our paper (1). The full package can be downloaded from GitHub (Rextinct), and will be soon also available as a Shiny app and on the CRAN.

Our package’s 3 functions (calendar, criwm, griwm) have a friendly syntax, with examples shown in the table below:

Download the package from GitHub to your local R space:
> install.packages(“devtools”)
> library(devtools)
> devtools::install_github(“FredSaltre/CRIWM/Rextinct”)

Create data files (e.g. in Excel) in working directory “dat1.txt” = text file with two columns (column 1 = ages, column 2 = errors); “dat2.txt” = text file with three columns (column 1 = ages, column 2 = errors, column 3 = age name or code)

Run function in R What it does

> calendar(“dat2.txt”, cal_curve = “marine20”) calibrates ¹⁴C ages for marine fossils (calibration curve = Marine20)

> criwm(“dat1.txt”) calculates extinction time with CRIWM for Northern Hemisphere, terrestrial fossils (calibration curve = IntCal20)

> griwm(“dat1.txt”, cal_curve = “shcal20”) calculates extinction time with GRIWM for Southern Hemisphere, terrestrial fossils (calibration curve = SHCal20)

Great stats do not correct for bad data

Finally, most C¹⁴ chronologies of animal species (certainly those from late Quaternary megafauna like mammoths, moas, rhinos, and saber-toothed cats) (22) are built from time series of ¹⁴C ages of the protein collagen preserved in fossilised skeletal materials (antler, bone, horncore, ivory, tooth). As with any quantitative analysis, the robustness of a statistical technique is independent of the quality of the source data. In other words, collecting and analysing such data are two different aspects, but the two are equally important in a research project: “… with good data, models could provide crucial insights about large-scale changes” in extinct megafauna (23).

We cautionthat CRIWM cannot correct for radiocarbon-dating inaccuracies. Those inaccuracies originate from ¹⁴C incorporated by fossil skeletal materials from their geological environments or introduced by chemicals used to curate fossils in museums or to process samples for radiocarbon dating. Geochronological labs can efficiently extract the collagen of fossils using acids and heat (24), but accelerator mass spectrometers cannot differentiate ¹⁴C isotopes that were part of the bone collagen before an organism died from those taken by the collagen after death. They are identical particles when it comes to counting exactly as two different coins are the same thing, even if we got one from a coffee machine and, one year later, the other from a bank.

The truth is that collagen is highly reactive with the soils and waters in which a skeleton is buried from centuries to millennia. As a result, fossils can incorporate alien ¹⁴C from carbon-rich compounds well after the animal perished. If those compounds are not removed, the measured ¹⁴C age of a fossil will be a combination of the true age of the fossil and the age of the contaminants. Removing contaminants, particularly soil humic acids chemically bound to collagen fibrils, requires sound protocols of chemical purification of collagen (24) – see blog post.

Accurate dating is therefore a must for building reliable chronologies for quantifying extinction time, regardless of the prowess of the statistical method chosen to estimate extinction.

Salvador Herrando-Pérez & Frédérik Saltré

Acknowledgements

Fred was supported by the Australian Research Council Centre of Excellence for Australian Biodiversity and Heritage (CE170100015). Salva was supported by and Australian Research Council Discovery Project (DP170104665) and the European Union’s LIFE Programme (LIFE18 NAT/ES/000121 LIFE DIVAQUA).

References

1. Herrando-Pérez, Saltré. 2024. Estimating extinction time using radiocarbon dates. Quaternary Geochronology 79: 101489
2. Swift et al. 2019. Micro methods for megafauna: novel approaches to Late Quaternary extinctions and their contributions to faunal conservation in the Anthropocene. Bioscience 69: 877-887
3. Hajdas et al. 2021. Radiocarbon dating. Nature Reviews Methods Primers 1: 62
4. Elias. 2023. Late Pleistocene megafaunal extinctions. Encyclopedia of Quaternary Science: 1-30
5. Raup. 1986. Biological extinction in Earth history. Science 231: 1528-1533
6. Signor III, Lipps. 1982 in Geological Implications of Impacts of Large Asteroids and Comets on the Earth, Silver, Schultz, Eds. (Geological Society of America), 190, 291-296
7. Hughen et al. 2004. ¹⁴C activity and global carbon cycle changes over the past 50,000 years. Science 303: 202-207
8. Pavón-Carrasco et al. 2018. Multi-centennial fluctuations of radionuclide production rates are modulated by the Earth’s magnetic field. Scientific Reports 8: 9820
9. Roth, Joos. 2013. A reconstruction of radiocarbon production and total solar irradiance from the Holocene ¹⁴C and CO₂ records: implications of data and model uncertainties. Climate of the Past 9: 1879-1909
10. Wang, Marshall. 2016. Estimating times of extinction in the fossil record. Biology Letters 12: 20150989
11. Boakes et al. 2015. Inferring species extinction: the use of sighting records. Methods in Ecology and Evolution 6: 678-687
12. Bradshaw et al. 2012. Robust estimates of extinction time in the geological record. Quaternary Science Reviews 33: 14-19
13. Reimer et al. 2020. The IntCal20 Northern Hemisphere radiocarbon age calibration curve (0-55 cal kBP). Radiocarbon 62: 725-757
14. Hogg et al. 2020. SHCal20 Southern Hemisphere calibration, 0-55,000 years cal BP. Radiocarbon 62: 759-778
15. Heaton et al. 2020. Marine20—the marine radiocarbon age calibration curve (0-55,000 cal BP). Radiocarbon 62: 779-820
16. Saltré et al. 2015. Uncertainties in dating constrain model choice for inferring extinction time from fossil records. Quaternary Science Reviews 112: 128-137
17. Lister, Stuart. 2019. The extinction of the giant deer Megaloceros giganteus (Blumenbach): new radiocarbon evidence. Quaternary International 500: 185-203
18. Marchenko et al. 2015. Paleodiet, radiocarbon chronology, and the possibility of freshwater reservoir effect for Preobrazhenka 6 burial ground, Western Siberia: preliminary results. Radiocarbon 57: 595-610
19. van der Plicht et al. 2015. New Holocene refugia of giant deer (Megaloceros giganteus Blum.) in Siberia: updated extinction patterns. Quaternary Science Reviews 114: 182-188
20. Brassey et al. 2013. More than one way of being a moa: differences in leg bone robustness map divergent evolutionary trajectories in Dinornithidae and Emeidae (Dinornithiformes). PLoS ONE 8: e82668. https://doi.org/10.1371/journal.pone.0082668
21. Holdaway et al. 2014. An extremely low-density human population exterminated New Zealand moa. Nature Communications 5: 5436. https://doi.org/10.1038/ncomms6436.
22. Stuart (2015). Late Quaternary megafaunal extinctions on the continents: a short review. Geological Journal 50: 338-363
23. Price et al. 2018. Big data little help in megafauna mysteries. Nature 558: 23-25
24. Herrando-Pérez. 2021. Bone need not remain an elephant in the room for radiocarbon dating. Royal Society Open Science 8: 201351