I meant to get this out yesterday, but was too hamstrung with other commitments. Now the media circus has beat me to the punch. Despite the lateness (in news-time) of my post, my familiarity with the analysis and the people involved gives me a unique insight, I believe.
So a couple of months ago, Fangliang He and I were talking about some new analysis he was working on where he was testing the assumption that back-casted species-area relationships (SAR) gave reasonable estimates of inferred extinction rates. Well, that paper has just been published in today’s issue of Nature by Fangliang He and Stephen Hubbell entitled: Species–area relationships always overestimate extinction rates from habitat loss (see also the News & Views piece by Carsten Rahbek and Rob Colwell).
The paper has already stirred up something of a controversy before the ink has barely had time to dry. Predictably, noted conservation biologists like Stuart Pimm and Michael Rosenzweig have already jumped down Fangliang’s throat.
Extinction rates of modern biota in the current biodiversity crisis (Ehrlich & Pringle 2008) are wildly imprecise. Indeed, it has been proposed that extinction rates exceed the deep-time average background rate by 100- to 10000-fold (Lawton & May 2008; May et al. 1995; Pimm & Raven 2000), and no rigorously quantification of these rates globally has ever been accomplished (although there are several taxon- and region-specific estimates of localised extinction rates (Brook et al. 2003; Regan et al. 2001; Hambler et al. 2011; Shaw 2005).
Much of the information used to infer past extinction rate estimates is based on the species-area relationship (e.g., Brook et al. 2003); this method estimates extinction rates by reversing the species-area accumulation curve, extrapolating backward to smaller areas to calculate expected species loss. The concept is relatively simple, even though the underlying mathematics might not be.
The basic species-area relationship is a power function of the form: S = cAz
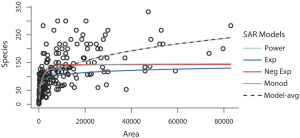
Figure 1. Multiple species-area relationship (SAR) models applied demonstrating model uncertainty (Giam et al. 2011)
where S = the number of species in a broad habitat type of area A, and c and z are estimated constants. Not only are there are various modifications of the underlying model (e.g., the exponential, negative exponential and monod forms – Giam et al. 2011; Guilhamon et al. 2008) (Fig. 1), they can be combined them using both Bayesian and maximum-likelihood approaches to provide model-averaged predictions of species accumulation with habitat area (Giam et al. 2011). Such an approach ensures that model uncertainty is also incorporated into the models that are known to rank differently depending on region and taxon modelled (Giam et al. 2011).
The approach to estimate extinctions generally takes the basic form of the power model above and adjusts it based on a difference between an ‘original’ time t and some modified (i.e., lost habitat) time t+1:
St+1/St = c(At+1/At)z
However, in 2010, this approach had a major paradigm shift (Koh & Ghazoul 2010; Koh et al. 2010). The first problem in the above approach assumes that the land use between the habitat areas being modelled (i.e., the ‘matrix’) are completely inhospitable to any species considered; the second assumes that there are no deleterious effects of the matrix on the habitat fragments (i.e., ‘edge effects’). A modified approach therefore corrects simultaneously for taxon-specific responses to individual components of the landscape matrix (Fig. 2) by adjusting the power coefficient (z), and for the matrix ‘edge effects’ on the At+1 term:
St+1/St = c((At+1/- δ ∑Mβj)/At)γ∑Npiσi
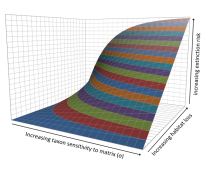
Figure 2. Matrix-calibrated species-area relationship model (Koh & Ghazoul 2010)
where bj = the edge-affected area of the jth habitat fragment, M = the total number of fragments, δ = the declining function of the edge effect as perceived by the taxon (e.g., δ = 0.5 if edge effect declines linearly with distance from habitat margin), γ = a constant that reflects the rate of change in species number per unit area on true island archipelagos, σ = an area-weighted average of taxon-specific responses to matrix components, p = the proportional area of the ith matrix component relative to the total area of the matrix, and N = the total number of matrix components (Koh & Ghazoul 2010; Koh et al. 2010).
Now He & Hubbell (2011) set to challenge all extinction rate estimates based on species-area relationships. The problem is rather obvious, but has failed to be appreciated because the power function has no sampling theory relating it to species distributions.
The species-area relationship essentially estimates the area required to sample the first individual of a species, whereas the endemics-area relationship is its mirror image and the area required to sample the last individual of that species (Fig. 3). This essentially allows for the estimation of extinction based on the loss of habitat area. However, the mirror image assumption is false when a species’ individuals are clumped (i.e., not randomly distributed), which is nearly ubiquitous in nature (Condit et al. 2000). Thus, the area that must be added to find the first individual of a species in general is much smaller than the area that must be removed to eliminate the last individual of a species. Therefore, on average it takes a much greater loss of area to cause the extinction of a species than it takes to add the species on first encounter, and this result holds regardless of how well the power-law species-area function fits species-area data.
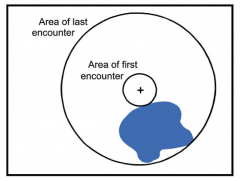
Figure 3. Range distribution of a species (blue area), and an arbitrary starting sample point, indicated by +. Regardless of starting location, a sampling frame of arbitrary shape (here circular) with an area of a size sufficient to contact the species for the first time is always less than the sample area needed to encompass the entire range of the species (He & Hubbell 2011)
He & Hubbell (2011) estimated in a few examples that species extinctions are over-estimated by about 75 %, but this is likely to be taxon- and region-specific.
Now, this is exciting in its own right, but the story isn’t finished. I think the next step is to attempt to combine model uncertainty, matrix calibration and the EAR bias. Instead of complaining that the He & Hubbell approach negates recent developments, it should be viewed instead as another way to improve existing models. Better predictions of land-use change over the coming century, and the state-of-the-art species-area models, should be able determine the degree of bias in extinction predictions.
Of course, there are potentially some issues that remain unresolved. In speaking with some colleagues about the He & Hubbell paper, it seems that it might only be implemented with associated distribution data. Where these are not available or not of high enough quality, then perhaps the approach is not useable.
Another concern arises from the calculation of z itself – if it is estimated from species reduction observations after land-use change rather than accumulation curves, it could better reflect extinctions in the backward calculation. Thus, the bias proposed by He & Hubbell might not be as great as they claim.
So, expect a battery of critiques and responses to this article. Exciting stuff, indeed.
References
- Brook BW, Sodhi NS, Ng PKL, Catastrophic extinctions follow deforestation in Singapore Nature 424, 420 (2003)
- Condit R, Ashton PS, Baker P, Bunyavejchewin S, Gunatilleke S, Gunatilleke N, Hubbell SP, Foster RB, Itoh A, LaFrankie JV, Lee HS, Losos E, Manokaran N, Sukumar R, Yamakura T, Spatial patterns in the distribution of tropical tree species Science 288, 1414 (2000)
- Ehrlich PR, Pringle RM, Where does biodiversity go from here? A grim business-as-usual forecast and a hopeful portfolio of partial solutions Proc Natl Acad Sci USA 105, 11579 (2008)
- Giam X, Sodhi NS, Brook BW, Tan HTW, Bradshaw CJA, Relative need for conservation assessment of vascular plant species among ecoregions J Biogeogr 38, 55 (2011)
- Guilhaumon F, Gimenez O, Gaston KJ, Mouillot D, Taxonomic and regional uncertainty in species-area relationships and the identification of richness hotspots Proc Natl Acad Sci USA 105, 15458 (2008)
- Hambler C, Henderson PA, Speight MR, Extinction rates, extinction-prone habitats, and indicator groups in Britain and at larger scales Biol Conserv 144, 713 (2011)
- Koh LP, Ghazoul J, A matrix-calibrated species-area model for predicting biodiversity losses due to land-use change Conserv Biol 24, 994 (2010)
- Koh LP, Lee TM, Sodhi NS, Ghazoul J, An overhaul of the species–area approach for predicting biodiversity loss: incorporating matrix and edge effects J Appl Ecol 47, 1063 (2010)
- May RM, Lawton JH, Stork NE, in Extinction rates, edited by J. H. Lawton and R. M. May (Oxford University Press, Oxford, 1995), pp. 1
- Pimm SL, Raven P, Extinction by numbers Nature 403, 843 (2000)
- Regan HM, Lupia R, Drinnan AN, Burgman MA, The currency and tempo of extinction Am Nat 157, 1 (2001)
- Shaw P, Estimating local extinction rates over successive time-frames Biol Conserv 121, 281 (2005)
