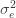New Paper on Genomics

James Lee and I have a new paper out: Lee and Chow, Conditions for the validity of SNP-based heritability estimation, Human Genetics, 2014. As I summarized earlier (e.g. see here and here), heritability is a measure of the proportion of the variance of some trait (like height or cholesterol levels) due to genetic factors. The classical way to estimate heritability is to regress standardized (mean zero, standard deviation one) phenotypes of close relatives against each other. In 2010, Jian Yang, Peter Visscher and colleagues developed a way to estimate heritability directly from the data obtained in Genome Wide Association Studies (GWAS), sometimes called GREML. Shashaank Vattikuti and I quickly adopted this method and computed the heritability of metabolic syndrome traits as well as the genetic correlations between the traits (link here). Unfortunately, our methods section has a lot of typos but the corrected Methods with the Matlab code can be found here. However, I was puzzled by the derivation of the method provided by the Yang et al. paper. This paper is our resolution. The technical details are below the fold.

The additive genetic contribution to a trait can be quantified with the linear model

(*)

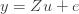
where

is an

dimensional vector of phenotypic values,

is an

$n\times p$

matrix of standardized genotypes,

is an

dimensional vector of additive genetic coefficients, and

is the

dimensional vector of residuals, which includes effects of the environment, nonlinear genetic effects and interactions.

is like the noise term in linear regression. If the phenotypes are standardized, and we have a large enough sample size, then the variance of the phenotypes is approximately

$y'y/n = u'Z'Zu/n+ e'e/n = \sigma_A^2 + \sigma_e^2$

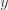
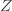
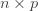
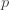
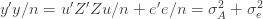
where the cross terms are zero. Here, I use statistical notation where prime means transpose. Technically, I should take the expectation value over the distribution of

but I will be completely non-rigorous here. The second equality can be arrived at if we assume that SNPs on the GWAS chip are uncorrelated (i.e. in linkage equilibrium) so that

is approximately the identity matrix and the inner product

is thus the sum of the variances at each SNP, which equals the total additive variance

$\sigma_A^2$

on the GWAS chip set and

$\sigma_e^2$

is the residual variance. If the phenotypes are standardized then the narrow-sense heritability is

$h_g^2 = \sigma_A^2$

. Yang et al. made the suggestion that the additive variance could be estimated directly by considering (*) to be a mixed-linear model and fitting the covariance model

$yy' = A\sigma_A^2 +I_n\sigma_e^2$

(**)

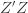
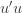
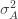
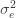
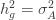
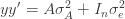
to the data via restricted maximum likelihood. Here,

is the

$n\times n$

dimensional relationship matrix (i.e it is the genetic covariance matrix). However, note that this relationship implicitly implies that

is equivalent to

, which is not a mathematical necessity and as we show in the paper not even approximately true. The way that Yang et al. justified this assertion was that they considered the regression coefficients

to be a set of uncorrelated random variables and thus

is proportional to the identity matrix. However, this assertion puzzled me because the regression coefficients are not supposed to be random variables with identical variance. Yet the method has been validated in multiple ways. It took us awhile but James and I eventually figured out why it works.

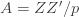
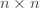
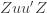
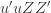
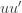
Equation (**) is a mixed linear model, which is fit to the data using restricted maximum likelihood (REML). However, if we assume that the phenotypes are standardized and there are no other covariates then this reduces to simple maximum likelihood with log of the likelihood:

$L = -\frac{n}{2}\log 2\pi - \frac{1}{2}\log|V|- \frac{1}{2} y'V^{-1}y$

(***)

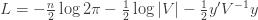
Differentiating (**) by

$\sigma_A^2$

and

$\sigma_e^2$

and setting to zero gives the maximum likelihood conditions

$Tr(V^{-1})=y'V^{-1}V^{-1}y$

$Tr(V^{-1}A)=y'V^{-1}AV^{-1}y$

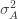
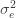
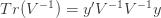
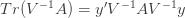
These equations are usually solved numerically with some sort of iteration scheme. However, if we consider the limit where

$\sigma_A$

is very small then we can use the matrix inverse approximation

$V^{-1}\approx \sigma_e^{-2}\left(I-\frac{\sigma_A^2}{\sigma_e^2}A\right)$

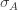
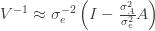
Substituting this back into (***) and solving for

$\sigma_A^{2}$

and using

$\sigma^2_A+\sigma_e^2=1$

we get the condition

$\sigma_A^2 = 1-\frac{1}{n}y'Ay$

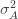
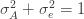
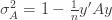
We thus find that a necessary condition for the maximum likelihood (***) to yield the correct estimate for

$\sigma_A^2$

is if

$y'Ay/n=\sigma_e^2$

. If we substitute (*) and the definition of A back into this condition we get

$(e'+u'Z')ZZ'(Zu+e)/p=\sigma_e^2$

(****)

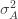
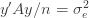
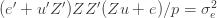
If we take the (****) term by term, we find that

$e'ZZ'e \approx \sigma_e^2$

if the genotypes are standardized. By the properties of regression, we also get that

(i.e. fitted line and residuals are orthogonal). Finally, if the GWAS markers are all uncorrelated (i.e. linkage equilibrium) then we have

is the identity so

$u' Z'ZZ'Zu/p=(n/p)\sigma_A^2$

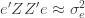
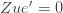
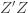
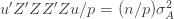
which is assumed to be small compared to

$\sigma_e^2$

. However, linkage equilibrium is not necessary for GREML to give good estimates. What we show in the paper is that as long as the correlations between markers is fairly uniform, then it still works well. It’s only if some markers are highly correlated with others while others are not that you can run into problems.

Biology Magazine

New Paper on Genomics

About the author

Author's Latest Articles

Magazines

COMMUNITY BIOLOGY