Figures and chart taken from the snappily titled On the average temperature of airless spherical bodies and the magnitude of Earth’s atmospheric thermal effect by Ned Nikolov and Karl Zeller, who are "climate contrarians", to put it mildly.
-------------------------------------------------
I have been having an email spat with an Alarmist and a Lukewarmer over what is the best way to estimate a planet's surface temperature (i.e. calculate the Effective Temperature).
1. The IPCC approach is to take incoming solar radiation per m2 (adjusted for albedo) on the day side and average over the whole planet at once, then do the usual calc's.
2. The scientific approach is to take the incoming solar radiation (adjusted for albedo) on the day side, then do the usual calc's to find day-side temperature; then work out how quickly it cools on the night side to find out average night-side temperature; and then average the two.
Each approach has some arguments in favour and against, but surely the tie-breaker is "which result matches actual observations more closely?" and then we use that approach in future.
-----------------------------------------------
The Moon has no atmosphere (or clouds or oceans) to confuse things, so let's use it as an example. The article includes the following diagram (click to enlarge):
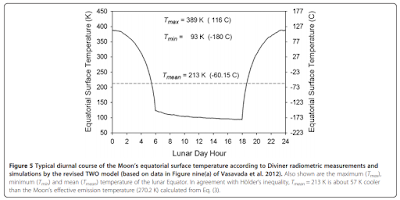
Agreed facts - peak incoming solar radiation overhead at equator at noon = 1,370, albedo 0.05*= 1,300 W/m2 which affect the temperature of the surface.
* The official figure is 0.12, but at the Equator, sunlight is less likely to bounce off than if it hits the surface at a flat angle near the Poles.
--------------------------------------------
1. The IPCC approach is, 1 m2 at the equator gets an average of half the peak value during the day = 650 W/m2 and during the night it gets none at all, so on average over a whole lunar day it gets 325 W/m2. Divide by 5.67, times by 10^8, take the fourth root = effective temperature 275 K.
That's clearly wildly out. The actual average is 213K.
--------------------------------------------
2. The scientific approach is:
a) Peak day-time temp = (1,300 ÷ 5.67 x 10^8)^0.25 = 389K. That's an excellent match.
b) Average day-time temp (based on average radiation during the day i.e. half of 1,300 W/m2*)
= (650 ÷ 5.67 x 10^)^0.25 = 327K. That's quite close to the temperature at afternoon-evening (Lunar Hour 3) and in the mid-morning (Lunar Hour 21).
(* It would be better to calculate the temp for every hour and average those, but that's a right old faff and adds little by way of accuracy, and that is not the point of this post).
c) Average night-time temp has nothing to do with incoming solar radiation (there is none!), you have to work out the "stock" of thermal energy at sunset and work out how quickly it radiates away, the "flow".
The temp at sunset = 120K (by looking at the chart), which falls to 93K just before sunrise. 22% of it's "stock" has "flowed away" during the night. Average temp 107K. We know the answers, we just have to make sense of them and put them in context:
Let's assume it's the top 6" which warms up and cools down (like on Earth).
For each m2, that's about 340 kg mass (not 'weight'!) of rock.
Let's assume specific heat capacity of lunar rock is the same as Earth rocks at very low temperatures = 1,000 J/kg/K.
(these variables are to illustrate the point, I had to guesstimate)
The temp at sunset = 120K
So the "stock" of heat at sunset per m2 = 340kg x 1,000 J/kg/K x 120K = 41 million Joules.
During the night, it is emitting 107K^4 ÷ 10^8 x 5.67 = 7.4 W/m2 (same calculation as above, just in reverse).
Over two Earth weeks, it loses 7.4/m2 x 3,600 secs/hour x 336 hours = 9 million Joules.
That's the "flow".
Check: 9 million divided by 41 million = 22%, job done.
d) We then average the day-time average from b) and the night-time average from c) and get 217K, which is pretty close to the mathematical average 213K.
So... which is the better method - the IPCC approach or the scientific approach?
Answers on a postcard (or in the comments).
