I’ve been asked in a comment to give a sample of pseudo code for an MCMC algorithm to fit a linear model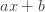 
to some data. See here for the original post on MCMC. With a linear model, you can write down the answer in closed form (see here), so it is a good model to test your algorithm and code. Here it is in pseudo-Julia code:
# initial guess for parameters a and b
a=0
b=0
# construct chi squared, where D is the data vector and x is the vector of the
# independent quantity
chi = norm(D - (a*x +b))^2;
for n = 1 : total;
# Make random guesses for new normally distributed a and b with mean old a and b
# and standard deviation asig and bsig
at = a + asig * randn()
bt = b + bsig * randn() chit = norm(D - (at*x + bt))^2;
# Take ratio of likelihoods, sigma is the data uncertainty
ratio=exp((-chit + chi)/(2*sigma^2));
# Compare the ratio to a uniform random number between 0 and 1,
# keep new parameters if ratio exceeds random number
if rand() < ratio a = at;
b = bt; chi = chit; end
end
# Keep running until convergence
