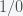Math Solved Zeno’s Paradox

On some rare days when the sun is shining and I'm enjoying a well made kouign-amann (my favourite comes from b.patisserie in San Francisco but Patisserie Poupon in Baltimore will do the trick), I find a brief respite from my usual depressed state and take delight, if only for a brief moment, in the fact that mathematics completely resolved Zeno's paradox. To me, it is the quintessential example of how mathematics can fully solve a philosophical problem and it is a shame that most people still don't seem to know or understand this monumental fact. Although there are probably thousands of articles on Zeno's paradox on the internet (I haven't bothered to actually check), I feel like visiting it again today even without a kouign-amann in hand.

I don't know what the original statement of the paradox is but they all involve motion from one location to another like walking towards a wall or throwing a javelin at a target. When you walk towards a wall, you must first cross half the distance, then half the remaining distance, and so on forever. The paradox is thus: How then can you ever reach the wall, or a javelin reach its target, if it must traverse an infinite number of intervals? This paradox is completely resolved by the concept of the mathematical limit, which Newton used to invent calculus in the seventeenth century. I think understanding the limit is the greatest leap a mathematics student must take in all of mathematics. It took mathematicians two centuries to fully formalize it although we don't need most of that machinery to resolve Zeno's paradox. In fact, you need no more than middle school math to solve one of history's most famous problems.

The solution to Zeno's paradox stems from the fact that if you move at constant velocity then it takes half the time to cross half the distance and the sum of an infinite number of intervals that are half as long as the previous interval adds up to a finite number. That's it! It doesn't take forever to get anywhere because you are adding an infinite number of things that get infinitesimally smaller. The sum of a bunch of terms is called a series and the sum of an infinite number of terms is called an infinite series. The beautiful thing is that we can compute this particular infinite series exactly, which is not true of all series.

Expressed mathematically, the total time

it takes for an object traveling at constant velocity to reach its target is

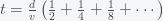
which can be rewritten as

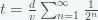
where

is the distance and is the velocity. This infinite series is technically called a geometric series because the ratio of two subsequent terms in the series is always the same. The terms are related geometrically like the volumes of n-dimensional cubes when you have halve the length of the sides (e.g. 1-cube (line and volume is length), 2-cube (square and volume is area), 3-cube (good old cube and volume), 4-cube ( hypercube and hypervolume), etc) .

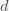
For simplicity we can take

. So to compute the time it takes to travel the distance, we must compute:

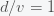
To solve this sum, the first thing is to notice that we can factor out

and obtain

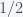
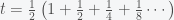
The quantity inside the bracket is just the original series plus 1, i.e.

and thus we can substitute this back into the original expression for

and obtain

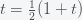
Now, we simply solve for

and I'll actually go over all the algebraic steps. First multiply both sides by 2 and get

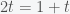
Now, subtract

from both sides and you get the beautiful answer that . We then have the amazing fact that

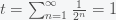
I never get tired of this. In fact this generalizes to any geometric series

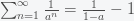
for any

that is less than 1. The more compact way to express this is

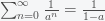
Now, notice that in this formula if you set

, you get , which is infinity. Since for any , this tells you that if you try to add up an infinite number of ones, you'll get infinity. Now if you set you'll get a negative number. Does this mean that the sum of an infinite number of positive numbers greater than 1 is a negative number? Well no because the series is only defined for , which is called the domain of convergence. If you go outside of the domain, you can still get an answer but it won't be the answer to your question. You always need to be careful when you add and subtract infinite quantities. Depending on the circumstance it may or may not give you sensible answers. Getting that right is what math is all about.