As a fun maths challenge, I decided to apply the principles outlined in Acceleration ≈ gravity and see whether I could get sensible results by applying basic maths, basic physics and common sense.
You are told (taken from the US standard atmosphere):
1. Pressure at sea level = 101.325 Pa
2. Temperature at sea level = 288 K
3. Density at sea level = 1,200 kg/m3 (a bit on the low side?)
T, D and P are closely interdependent, but you need one more fixed point. If you are told the real-world lapse rate (and certain other constants), you can do it the long way round by using Barry to find pressure at each altitude; then estimating temperature at altitude by subtracting the real-world lapse rate from 288 K; and then using P and T to calculate D.
If you are also told that D at the top of the troposphere (10 km altitude for simplicity) = 400g/m3, it's actually much easier. You can interpolate everything else, including the likely lapse rate.
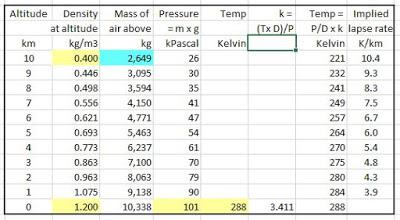
1. Set up your Excel sheet, type in the given numbers (pale yellow)
2. You can assume that density changes in straight line, but it is more realistic to assume it changes geometrically, so it goes up by a factor of 1.011 (3^0.1) for each km lower (doesn't make much difference)
3. Then work out the 'mass of the air' above. The mass of air between 0 and 10 km altitude is simple addition of the densities of the air in each km-high slice above it x 1,000 (density per km height = 1,000 x D at that altitude) plus the mass of air in the stratosphere etc (balancing figure)
4. We know that the total mass of air must be enough to create a pressure of 101,325 Pa at sea level, so it must be 101,325/9.801 ≈ 10,338 kg total, so you put in 2,649 kg (pale blue) as a balancing figure to get it to add up to 10,338 kg.
5. Pressure is simply 'mass of air above that altitude' x gravity (9.801 m/s2) per m2, so e.g. at 9 km, it's 2,649 kg + (446 g/m3 x 1,000 m) = 3,095 kg x 9.801 = 26 kPa
6. Temperature ∝ pressure/density i.e. temperature = pressure/density x constant 'k'
7. Work out 'k' = (288 x 1.2)/101 = 3.411 in this example
8. Temperature at each altitude = pressure/density at that altitude x 3.411.
The results match the Standard Atmosphere very well. The T, and P results for top of troposphere are pretty bang-on. It does show that the lapse rate is lower than the accepted mid-figure 6.5 K/km at low altitudes and higher at higher altitudes. This is not unrealistic, as there is more absolute humidity at lower altitudes, but that's probably a happy accident and it averages out to ~6.5 K/km overall:
All this neither proves nor disproves the Physics Denier's contention that sea level temperature would be ~33 degrees cooler without 'greenhouse gases' (disproving that is far simpler and requires little or no maths, just facts and logic), but I love a maths challenge.
------------------------------------------
These workings also give a good understanding of the real world, against which you can test various Physics Denier theories - like the 'Top Of Atmosphere' theory, which says the temperature at the Effective Emitting Altitude (about 5 to 6 km up) is fixed at 255K, but sea level temperatures are 33 degrees warmer than that solely because of 'greenhouse gases'. This is an alternative explanation for the observed lapse rate of ~6.5 K/km, but it has to be that much anyway because of gravity, in other words... the 'Top of Atmosphere' theory assumes that gravity doesn't exist.
Or do they mean that without greenhouse gases, the Effective Emitting Altitude would be sea-level (so sea level temperature would be 255K) and the gravity-induced lapse rate would stay much the same? On Mars, there is about forty times as much CO2/m3 as there is on Earth, but the Greenhouse Effect is negligible on Mars (5 degrees at most) and the Effective Emitting Altitude is no higher than it is on Earth. So that can't be it either. Hmm.
Debate Magazine
