How Income Inequality Can Affect GDP

Since income inequality is a big issue in the United States and the upcoming election, I thought it would be instructive to look at how income inequality may affect the total US income (GDP) in a very simple model. This will only be a linear model in the sense that I will model domestic spending given some income without demanding self-consistency so spending equals income. However, I think the same qualitative results will hold. Let us suppose that the a person's spending as a function of income 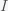is given by 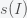. Now let 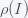be the distribution of income (i.e probability density function). The national income is then 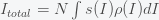, where 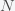is the US population. We can write this as , where the bar denotes expectation value or average. So income inequality is measured by how wide 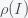is. A perfectly equal society would have 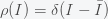. Now let's first suppose that 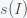is linear so your spending is exactly proportional to your income. In this case, 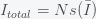, for any distribution and thus income inequality does not affect GDP. You will always get a GDP equal to spending at the US average. Now suppose that spending is super-linear or convex so you spend more as you earn more faster than you earn it. This assumes that you save less the richer you are. In this case, by Jensen's inequality , and the total GDP is bigger than if everyone spent at the average. In this case, income inequality would actually increase the pie. Now, finally in the case where the spending function is concave, you spend less as you earn more, or save more as you earn more then 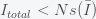, and thus the total spending is less than spending at the average. In this case, income inequality would reduce the GDP. So depending on how spending changes with income, income inequality could decrease or increase the size of the pie. My guess is that spending functions are concave so a little more equality could improve the economy.