
Adèle (c) Samantha Groenestyn (oil on linen)
Importing mathematics into painting has some potentially grand implications. The idea makes me flush with uncontainable excitement; it smacks of Descartes (2006 [1637]: 9) and his methodical approach to knowledge, and I would echo his rationalist sentiment: ‘I was most keen on mathematics, because of its certainty and the incontrovertibility of its proofs.’ This unlikely marriage between mathematics and painting is especially dear to me because it offers something steady and dependable in terms of color and not merely in terms of drawing; it promises to embrace the entirety of painting with its sober orderliness. This systematisation hardly destroys the poetry of painting. Rather, it allows us to sharpen our technical methods, which equips the genius (of the Kantian flavour) to paint something deeply insightful and moving. And it promises a double elegance: the sight of the painting itself, just like the sounds in music, may please us, and at the same time be grounded in delightfully crisp mathematical relationships, just like the improbable mathematical elegance of harmony in music.
These longings for order and systematisation sound rather like seventeenth-century aspirations to elevate painting to a science, or at least to a liberal art, which has much to do with shedding its humble craft status, as a trade practiced by illiterates. Painting has certainly made many efforts in this direction; it may boast of its academic status now that it is so commonly taught in universities rather than in ateliers, now that it defends itself verbally and indeed often consists more in its verbal conception and explanation than in its visual execution. But perhaps these victories are no victories at all: they strip painting of the very things that distinguish it as painting. Painting might have done better to have sought an intellectual ally in mathematics rather than in language, for there it would have found ways to describe its visual concepts succinctly and precisely.

Copy after Rodin, Burgher of Calais
This camaraderie is most apparent when it comes to color. Colour is the rogue that has been seized by painters who want to defy philosophical discourse, and it is the uncontainable element that philosophy has used to subordinate painting. It seems to defy principles, thus it eludes philosophers, and it seems to operate largely by inspiration, superstition and magic, which seems to be attractive to painters. Across both disciplines, there is general agreement that color is definitively not rule-amenable, while drawing is. Jacqueline Lichtenstein (1993 [1989]: 4; 62-3), in The Eloquence of Colour, traces this long-standing tension back to Plato and Aristotle, observing that ‘being material, color has always been seen as belonging to the ontologically deficient categories of the ephemeral and the random.’ Philosophy has, she writes, thus favoured the more conceptually manageable element of painting: drawing (Lichtenstein, 1989 [1993]: 4).
If color does not lend itself to principles, this has another, more practical, result. Philosophy aside, it means that color cannot be taught. This lends itself to all varieties of unwelcome mysticism, that I personally would like to see chased out of the discipline of painting. It suggests that painters are ‘gifted,’ that they are conduits for ‘inspiration,’ or that they must operate by chance–all of which deny that painting is a disciplined skill that can be developed and improved and harnessed for aesthetic purposes. This is an unhappy state for painting to be in, for it grants artists license to all sorts of nonsense and self-indulgence, and abuses the viewer with all manner of ineptly executed work. In short, it encourages carelessness and invites decadence. Painting is visibly decaying before our eyes.

Copy after Rodin, Burgher of Calais
In the face of these two apparent deficiencies, I want to argue that the emphasis on drawing–both as philosophically acceptable and as practically teachable–is misplaced. Drawing certainly does lend itself to principles which can indeed be taught, and perhaps this fact is even overplayed. There are elements to drawing that cannot be taught, because each draughtswoman will adapt the learned principles to her own sensibility; she will interpret them, introducing a quality of line that no one else has. And, more broadly, the principles that are discussed and taught are not incontestable facts of existence. This is very clearly described by Panofsky’s (1991 [1927]: 37) contrast of spherical and linear perspective. Lastly, I want to raise a surprisingly little-grasped fact, one that is also popularly rejected by painters: color is indeed amenable to principles, and there are painters who work with these principles and succeed in teaching them. Colour is very acutely described by geometry. In our infatuation with language, this straightforward ordering of color has persisted largely unnoticed for at least two hundred years.
Lichtenstein (1993 [1989]: 142) notes that ‘ever since society has set a hierarchy among human activities, their relation to language has been the ultimate criterion for the establishment of a division, both social and philosophical, between the noble arts and the servile trades.’ Because of this, she explains, painting has sought to prove itself by ‘literary credentials;’ in order to do this, it has been expected to ‘satisfy both theoretical and pedagogical objectives,’ as we have already considered (Lichtenstein 1993 [1989]: 142; 151). Since she accepts that color defies principles, she looks to rhetoric to redeem the intellectual status of painting, a fascinating move that demands more attention elsewhere, but we may here respond with our geometry of color.
Copy after Rodin, Burgher of Calais
A fascinating little tract by Philipp Otto Runge appeared in the early 1800s. His Farbenkugel, or ‘colour sphere,’ is a mathematically pure way of conceptualising color. It conceives of the relations between all colours three-dimensionally. He begins with a flat triangle that represents the three unmixed colours of red, yellow and blue. Each line is bisected to indicate that, mathematically, the secondary colours are the halfway points between each of these: orange, green and purple. These six points are extended out to the edges of a circle, which is then pierced by a perpendicular axis at whose poles stand white and black. The mid-point of this pole is, mathematically, a mid-tone gray. As colours move directly across the horizontal axis, they are neutralised by their mathematical opposite, entirely cancelling each other out as gray at the mid-point–yellow becomes, not more purplish, but more grey, as it moves towards purple, its opposite. Green and red exist in the same relation, and orange and blue. The knowledge of these relationships means a painter in fact need not use a black paint to recreate these relationships in paint: gray is not the absence of colour, but the annihilation of one color in its mathematical opposite–‘alle einander auf derselben Gerade gegenüberliegenden Farben [sind] als Kräfte anzunehmen, welche einander entgegenstehen und sich durch ihre Vermischung zerstören in Grau’ (‘all colours that lay across from each other on the same line are to be assumed opposing forces that, upon mixing, annihilate each other in grey’) (Runge, 1810: 28). The rest of the sphere is filled out by every conceivable mixed color and in every level of lightness and darkness, vividness and neutrality. The whole thing is most easily grasped visually, and this is the advantage of geometry.
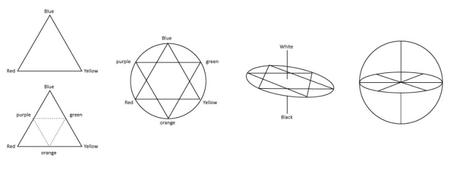
(After Philipp Otto Runge)
It is a very beautiful model, one developed concomitantly with discussions with Goethe, and a living idea still used and taught by artists who appreciate the more rugged borders of three-dimensional colour-space. But more than this, the emphasis on relationships allows a shift in thinking: rather than considering colours as absolutes, bound to precise recipes of two-parts cadmium yellow to one-part prussian blue, they may instead be managed and manipulated as a complex but entirely rational web of relationships. This means, in fact, an emancipation from the types of dogmas that more mystically-inclined painters tend to bark at other painters: it means a shift from objectively defining colours to subjectively experiencing them. It allows a painter to recreate her perceptual experience of seeing colours; it allows for the fact that a certain mixture can appear pink or green, depending on the context it is set in. It marks a dramatic difference between painters who ask ‘what color this really is,’ and those who ask how they perceive it. The second mindset affords far greater flexibility and dexterity with color. And it can be taught.

(From Philipp Otto Runge, Farbenkugel)
This kind of dexterity is important because ultimately, while we might define our concept of color in a pure mathematical way, paint itself does not respond to such precise geometrical divisions, and does not correspond so precisely to light. The painter must cope with two additional overlays to her mathematical concept of colour: the chemistry of paint and how the mixtures are achieved by actual pigments of vastly different physical properties, and the physics of light and the fact that her eyes take in a much broader gamut of colours than her paint is capable of mixing. A swift and nimble understanding of the relationships as geometric proportions is a solid conceptual ground that can be modified empirically as the painter’s experience with using paint and approximating it to what she sees grows. Runge (1810: 62) notes this as an aside to Goethe in one of his letters: ‘Ich kann mich hier nicht über die Praktik ausbreiten, weil es erstlich zu weitläufig wäre,’ (‘I cannot expand upon the practice here, firstly because it would ramble on too long,’) but he mentions that the artist requires ‘den nötigen chemischen wie mathematischen Kenntnissen’ (‘the necessary chemical alongside the mathematical knowledge.’)
Such systems equip us with knowledge, and thus confidence, and in the case of colour, adequately describe and organize the material reality of paint and at the same time accommodate our subjective, perceptual experience of it. Runge (1810: 42; 61) hopes that these pure insights will permit more definite expression; he thinks that being secure in the mental connections of the elements is the only means of setting a painter’s mind at ease, in the face of such superstition and chance. It would be well at this point to remind ourselves not to take the implications of these principles too far, and thus to return to Panofsky.

Copy after Claudel, Vertumne et Pomone
For the principles of vanishing-point perspective, the mainstay of principled drawing, are, indeed, a construction devised during the Renaissance, as Panofsky (1991 [1927]: 27) notes early on. It provides us with a mathematical space that is actually at odds with our perceptual experience of space, but that does not undermine its usefulness to us. Panofsky (1991 [1927]: 29-30) contrasts the visibly rigid ‘structure of an infinite, unchanging and homogenous space–in short, a purely mathematical space’ with ‘the structure of psychophysiological space.’ Our working concept of perspective demands that space conforms entirely to reason, that it is ‘infinite, unchanging and homogeneous’ (Panofsky (1991 [1927]: 28-9); but that demands certain assumptions that deny our experience of it: firstly, ‘that we see with a single and immobile eye,’ and secondly, that a flat plane adequately reproduces our curved optical image–two ‘rather bold abstractions’ from our perceptual experience.
‘In a sense,’ write Panofsky (1991 [1927]: 31), ‘perspective transforms psychophysiological space into mathematical space.’ And there is indeed nothing wrong with that if we recognize it as such, and do not take our theoretical underpinnings too far, thus over-emphasising the theoretical validity of drawing over color.
Copy after Claudel, Vertumne et Pomone
Beginning with (helpfully visual) geometric principles, we can thus devise rigorous and teachable theoretical systems for both of the equally important parts of painting, for drawing and for colour, describing them in pure, abstracted, mathematical terms, whose constancy is beautiful in and of itself. We can reclaim the liberal art of painting, award it some intellectual prestige, and even ground it in scientific principles that draw on chemistry and physics as well. Descartes’ project might not prove so alien in the murky and superstitious realm of painting.

Copy after Rodin, The sculptor and his muse
Lichtenstein, Jacqueline. 1993 [1989]. The Eloquence of Colour: Rhetoric and Painting in the French Classical Age. Translated by Emily McVarish. Berkeley: University of California.
Panofsky, Erwin. 1991 [1927]. Perspective as Symbolic Form. Translated by Christopher S. Wood. New York: Zone.
Runge, Philipp Otto. 1810. Farbenkugel: Konstruktion Des Verhältnisses Aller Mischungen Der Farben Zueinander Und Ihrer Vollständigen Affinität. Köln: Tropen.

