Numberphile did an interesting video on the models they use to predict the spread of viruses:
I reverse engineered their spreadsheet with a few basic assumptions to mirror their results (scaled up to UK population). The only variable we can seriously influence is how many people an infectious person infects every day ('daily rate').
The resulting curve is hyper-sensitive to any changes in the daily rate, so I can sort of understand why governments around the world have reacted the way they did.
At a daily rate of 1.5, it would take two years before the number of serious cases still in progress reaches 10,000. Less than 1.5, it just fizzles out.
To get the curve to match the growth in the number of cases recorded in the UK so far, the daily rate would have to be about 3, which - according to the model - would lead to a peak in serious cases of 2 million after ten weeks.
Here are three pairs of charts, showing population totals peak and the number of serious cases (assume one-tenth of those infected) for three different daily rates. The X-axis is just days from outbreak:
Daily rate 1.6
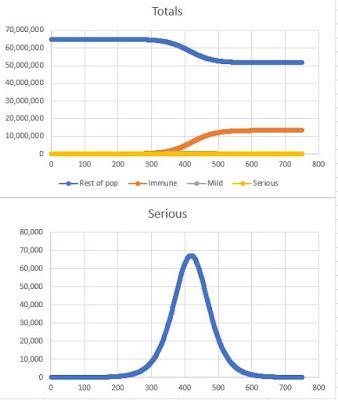
Daily rate 1.8
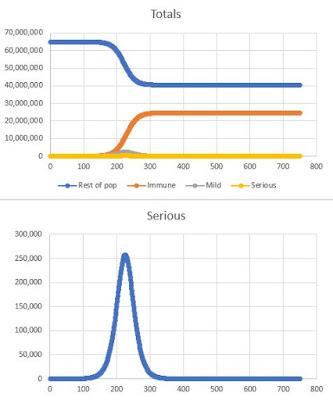
Daily rate 2.0
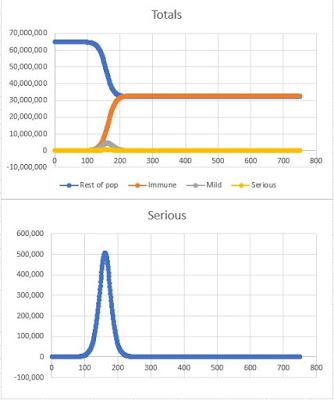
As mathematically enjoyable as all this is, I'm not sure those models are much use, beyond telling us that the lower the daily rate, the better.
In real life, the number of new cases which are recorded each day seems to flatten off after one or two months and then decline again. Worldinfo compiles all the available statistics country-by-country, including a chart of new cases recorded each day. Whether this flattening is because of all the lock downs, or whether it would have happened anyway, we will never know.
It also seems counter-intuitive that even with a high daily rate of 2.0, half the population (blue line) never gets it. That's because once half the population has had it and is immune, those who are infectious can only infect half as many each day as they could have done at the start. So the effective daily rate would fall to about 1, at which stage the whole thing fizzles out.
