Detecting an Asteroid

There were lots of collisions happened due to the asteroids coming from the outer space. Some incidents are very harmful for life on Earth. Now I try to investigate a new method to detect such asteroids coming from outer space and measure the velocity it moves.

We know there is relative motion of Earth with respect to the asteroid; due to Earth's spinning and due to the revolution of Earth around sun. We know when an asteroid is coming towards the Earth, some energized electromagnetic waves should come towards the Earth. And we detect and measure those electromagnetic waves at two different Earth times. Then within that two different Earth times, Earth has gone some length along the orbit of the Earth as well as it has rotated some angle around the rotating axis of the Earth. But basically the asteroid moves in a straight path with respect to other stellar object. i.e. relative to sun. The situation is as below.

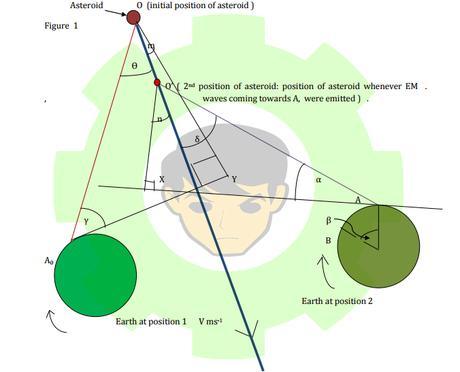
Where A 0 is the position that initial observation of asteroid and A is the 2 nd moment of asteroid detection and A and A 0 same position on Earth but at two different Earth times. And within that time interval Earth has rotated β angle around its axis of spinning. B is the position such that located left with respect to the rotating axis. And θ is the angle between A 0 O and asteroid coming direction. And γ is the angle between A 0 O and tangent line to Earth at A 0 (A 0 Y is the tangential line at point A 0 to the Earth and OY is the perpendicular line to A 0 Y). And AX is the tangential line to Earth at point A and O'X is the perpendicular line for line AX.
Earth spins about 360 degrees within 24 hours. Therefore
β = [2π/24) -/+ 2π/(365.25*24) ] * t ; t is the Earth time difference of detecting asteroid at two different moments. And (-/+) depends on the considering direction of revolving Earth around sun.
Let W is the tangential velocity of Earth at point A 0 , W' is the tangential velocity of Earth at point 'A' within space time. And U is the velocity of the asteroid with respect to 'Earth detection' at the first moment of detection at point A 0 . i.e. U was the velocity of the asteroid whenever now coming EM waves toward point A 0 were emitted. And U' is similar to the 2 nd detection of EM waves at point A. And important : U is the velocity component of V at A 0 in the direction A 0 Y and U' is also the velocity component of V, at position A, in the direction A 0 Y.
Then U = V cos(θ).cos(γ)...........................(1)
U' = - V'.cosδ.cos α.cos β. (minus include : because asteroid velocity component at the 2 nd detection is in the opposite direction of A 0 Y)
V' is the velocity of the asteroid with respect to the Earth ,whenever now coming(at the 2 nd detection of EM waves coming from the asteroid) EM waves were emitted. We can consider
V' =k.V k is a complex constant or function of V. Therefore
U' = -kV.cosδ.cos α.cos β........................(2)
β explanation :

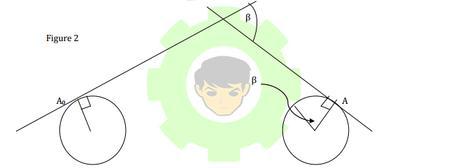
When Earth rotate β angle around its axis of rotation the tangential line at point A 0 should also rotate an angle β. Therefore angle between A 0 Y and AX is also β. Then the velocity component in the direction AX is equivalent to cos β times that velocity component and that is in the direction A 0 Y. When time value 't' is very small, we can neglect the second term of the expression for β. Because when t is very small, the angle Earth has gone around sun is negligible compare to the angle Earth has rotated around its axis within time t.
1. Due to axial rotation there is a tangential velocity component at point A 0 .
2. Due to the revolution around the sun , there is an another velocity component.
We know Earth has two velocity components.
0 Y ) = r 0 *(2π/365.25*24)* cos ϕ
1 )/24
Revolution component of velocity W (along the direction A
Explanation :

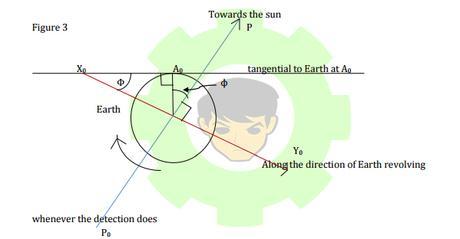
We know definitely PP 0 and XX 0 can be consider as perpendicular lines. Then we know that angle ϕ = (angular velocity * time taken to rotate the Earth about an angle ϕ). r 0 is the distance between sun and Earth when 2nd detection occurs. detection occurs.*(2π/365.25*24)* cos ϕ ].....................(3)) We have,
1 = time difference between the moment of asteroid 1st detection occurs and the time of the place such that the sun is overhead (whenever 1 st detection is occurring) That (t
Angular velocity of Earth to spin about its axis = 2π/T 1 ) can be easily measure: just the time difference between two clocks placed at A
time taken to rotate the Earth about an angle ϕ = t 0 and sun overhead position.
0 0 ' * (2π/365.25*24)*cos ϕ' *cos β
0 ' is the distance between sun and Earth whenever the 2 nd
2 is the time difference between the position of 2 nd detection occurs and similar sun overhead position.
Similarly revolution component of velocity W' along the direction A
0 0 ' * (2π/365.25*24)*cos ϕ' *cos β]...........................(4)
0 and the direction of asteroid observable; we can measure the angle γ. And by measuring the angle between the flat Earth surface at point A and the direction of asteroid observable ; we can directly measure the angle α.
0 (I
And ϕ' = (2π*t2/24) 1 ) by using suitable instrument as well as intensities of EM waves coming towards point A( I 2 1 , max and when δ →0, I 2 →I 2
Tangential velocity component of W = R(2π/24)
Tangential velocity component of W' = R(2π/24).cos β
R is the mean radius of the Earth.
Then, , max. Therefore using the equation of maximum intensity and the intensity equations for point A
W' = [ R(2π/24).cos β + r 0 and A, we can calculate the values of Ө and δ. Then we can get expressions for U and U' in terms of V. We can directly get the values of Wand W' as constant values. Let W= k 1 and W' = k 2 . Then the relative velocity of Earth with respect to the asteroid at position A
We can measure the values of γ and α : By measuring the angle between the flat Earth surface at point A 0 = V 1 = k 1 - g
We can measure the intensity of coming EM waves towards the point A 1 (V)..............................(5)
2 = k 2 - g 2 1
When Ө →0, I1 → I (V) is the expression get from equation (1) and g 2 (V) is the expression get from the equation (2). Then by relativistic Doppler formula we get
1 = [ 1/ √(1- (V1/C) ) ]. { 1- (W/U) }. f 0
f 2 = [ 1/ √(1- (V2/C) ) ]. { 1- (W'/U') }. f 0 '
Where f 1 is the frequency of coming EM waves toward point A 0 detected at point A 0 . And f 2 is similar frequency at point A. And f 0 is the real frequency of EM waves coming towards A 0 , when they were emitting. And f 0 ' is the real frequency of the EM waves coming towards A, when they were emitting by asteroid. Since time difference between two detection of asteroid is very small , we can consider f 0 = f 0 ' .Therefore by the above equations,
Then the relative velocity of Earth with respect to the asteroid at position A =

f 1 / f 2 = [ 1/ √(1- (V 1 /C) ) ]. { 1- (W/U) } / [ 1/ √(1- (V 2 /C) ) ]. { 1- (W'/U') }
Therefore we get the relation that contains V and k(V)terms. Therefore if we assume
k(V) =1( that means velocity of the asteroid does not change within that time interval of two detections occurs ), then we can estimate the value of V.
By substituting that V value to equation (1) we can find value of f 1 . And after that if we substitute that V value, to equation (2) and we can find value of f 2 . Then we get the difference of f 1 and f 2 . If f 1 < f 2 ; then we can conclude that that asteroid gradually becomes energize(may not be happened) , if f 2 < f 1 ; then we can conclude that the asteroid gradually becomes weaker in energy.
If we assume f 1 = f 2 directly, then by substituting that V value to both equations and by comparing those k(V) value with the integer orders of V value we got, we can get rough idea about the function k(V). Then by using some equations in relative motions and etc. we can estimate how far the asteroid from the Earth roughly.

Hi I am Geerasee. I am a contributing writter at Nerdynaut. Click to know more about me.