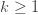As I promised in my previous post, here is a derivation of the analytic continuation of the Riemann zeta function to negative integer values. There are several ways of doing this but a particularly simple way is given by Graham Everest, Christian Rottger, and Tom Ward at this link. It starts with the observation that you can write
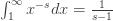
if the real part of
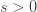 0" title="Analytic continuation continued" />0" class="latex" title="s>0" />. You can then break the integral into pieces with
0" title="Analytic continuation continued" />0" class="latex" title="s>0" />. You can then break the integral into pieces with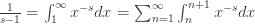
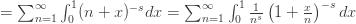
For
![x\in [0,1] x\in [0,1]](http://m5.paperblog.com/i/82/823924/analytic-continuation-continued-L-6FUV0b.jpeg)
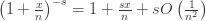
Now substitute (2) into (1) to obtain
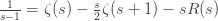
or
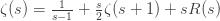
where the remainder
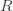
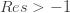 -1" title="Analytic continuation continued" /> -1" class="latex" title="Re s > -1" /> because the resulting series is absolutely convergent. Since the zeta function is analytic for
-1" title="Analytic continuation continued" /> -1" class="latex" title="Re s > -1" /> because the resulting series is absolutely convergent. Since the zeta function is analytic for 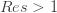 1" title="Analytic continuation continued" />1" class="latex" title="Re s >1" />, the right hand side is a new definition of
1" title="Analytic continuation continued" />1" class="latex" title="Re s >1" />, the right hand side is a new definition of 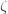
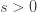 0" title="Analytic continuation continued" />0" class="latex" title="s >0" /> aside from a simple pole at
0" title="Analytic continuation continued" />0" class="latex" title="s >0" /> aside from a simple pole at 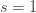
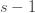
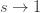
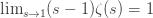
which implies that
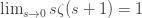
Taking the limit of

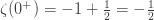
Hence, the analytic continuation of the zeta function to zero is -1/2.
The analytic domain of
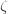
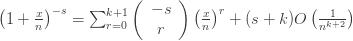
Inserting into (1) yields
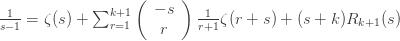
where
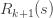
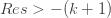 -(k+1)" title="Analytic continuation continued" />-(k+1)" class="latex" title="Re s>-(k+1)" />. Now let
-(k+1)" title="Analytic continuation continued" />-(k+1)" class="latex" title="Re s>-(k+1)" />. Now let 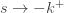
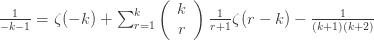
Rearranging (5) gives
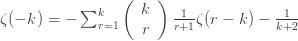
where I have used
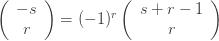
The righthand side of (6) is now defined for
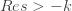 -k" title="Analytic continuation continued" /> -k" class="latex" title="Re s > -k" />. Rewrite (6) as
-k" title="Analytic continuation continued" /> -k" class="latex" title="Re s > -k" />. Rewrite (6) as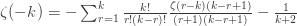
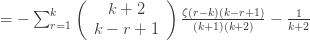
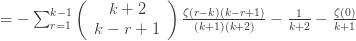
Collecting terms, substituting for
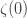
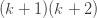
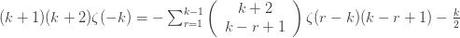
Reindexing gives
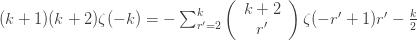
Now, note that the Bernoulli numbers satisfy the condition
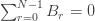
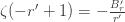
and obtain
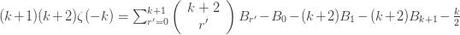
which using
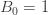
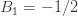
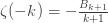
which is the analytic continuation of the zeta function for integers