Analytic Continuation

I have received some skepticism that there are possibly other ways of assigning the sum of the natural numbers to a number other than -1/12 so I will try to be more precise. I thought it would be also useful to derive the analytic continuation of the zeta function, which I will do in a future post. I will first give a simpler example to motivate the notion of analytic continuation. Consider the geometric series 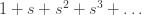$1+s+s^2+s^3+\dots$ . 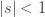If |s| < 1 < 1" title="Analytic continuation" />< 1" class="latex" title="|s| < 1" /> then we know that this series is equal to

$\frac{1}{1-s}$

(1)

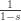
Now, while the geometric series is only convergent and thus analytic inside the unit circle, (1) is defined everywhere in the complex plane except at

. So even though the sum doesn’t really exist outside of the domain of convergence, we can assign a number to it based on (1). For example, if we set

we can make the assignment of

$1 + 2 + 4 + 8 + \dots = -1$

. So again, the sum of the powers of two doesn’t really equal -1, only (1) is defined at s=2. It’s just that the geometric series and (1) are the same function inside the domain of convergence. Now, it is true that the analytic continuation of a function is unique. However, although the value of -1 for

is the only value for the analytic continuation of the geometric series, that doesn’t mean that the sum of the powers of 2 needs to be uniquely assigned to negative one because the sum of the powers of 2 is not an analytic function. So if you could find some other series that is a function of some parameter

that is analytic in some domain of convergence and happens to look like the sum of the powers of two for some

value, and you can analytically continue the series to that value, then you would have another assignment.

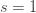
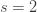
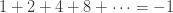
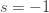
Now consider my example from the previous post. Consider the series

$\sum_{n=1}^\infty \frac{n-1}{n^{s+1}}$

(2)

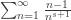
This series is absolutely convergent for

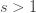1" title="Analytic continuation" />1" class="latex" title="s>1" />. Also note that if I set s=-1, I get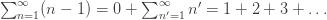

$\sum_{n=1}^\infty (n-1) = 0 +\sum_{n'=1}^\infty n' = 1 + 2 + 3 + \dots$

which is the sum of then natural numbers. Now, I can write (2) as

$\sum_{n=1}^\infty\left( \frac{1}{n^s}-\frac{1}{n^{s+1}}\right)$

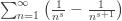
and when the real part of s is greater than 1, I can further write this as

$\sum_{n=1}^\infty\frac{1}{n^s}-\sum_{n=1}^\infty\frac{1}{n^{s+1}}=\zeta(s)-\zeta(s+1)$

(3)

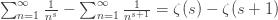
All of these operations are perfectly fine as long as I’m in the domain of absolute convergence. Now, as I will show in the next post, the analytic continuation of the zeta function to the negative integers is given by

$\zeta (-k) = -\frac{B_{k+1}}{k+1}$

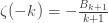
where

are the Bernoulli numbers, which is given by the Taylor expansion of

$\frac{x}{e^x-1} = \sum B_n \frac{x^n}{n!}$

(4)

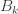
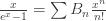
The first few Bernoulli numbers are

. Thus using this in (4) gives

$\zeta(-1)=-1/12$

. A similar proof will give

$\zeta(0)=-1/2$

. Using this in (3) then gives the desired result that the sum of the natural numbers is (also) 5/12.

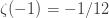
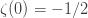
Now this is not to say that all assignments have the same physical value. I don’t know the details of how -1/12 is used in bosonic string theory but it is likely that the zeta function is crucial to the calculation.

Biology Magazine

Analytic Continuation

About the author

Author's Latest Articles

Magazines

COMMUNITY BIOLOGY