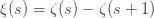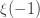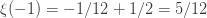Nonuniqueness of -1/12

I’ve been asked to give an example of how the sum of the natural numbers could lead to another value in the comments to my previous post so I thought it may be of general interest to more people. Consider again 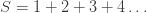$S=1+2+3+4\dots$ to be the sum of the natural numbers. The video in the previous slide gives a simple proof by combining divergent sums. In essence, the manipulation is doing renormalization by subtracting away infinities and the left over of this renormalization is -1/12. There is another video that gives the proof through analytic continuation of the Riemann zeta function

$\zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}$

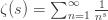
The zeta function is only strictly convergent when the real part of s is greater than 1. However, you can use analytic continuation to extract values of the zeta function to values where the sum is divergent. What this means is that the zeta function is no longer the “same sum” per se, but a version of the sum taken to a domain where it was not originally defined but smoothly (analytically) connected to the sum. Hence, the sum of the natural numbers is given by

$\zeta(-1)$

and

$\zeta(0)=\sum_{n=1}^\infty 1$

, (infinite sum over ones). By analytic continuation, we obtain the values

$\zeta(-1)=-1/12$

and

$\zeta(0)=-1/2$

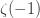
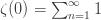
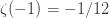
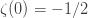
Now notice that if I subtract the sum over ones from the sum over the natural numbers I still get the sum over the natural numbers, e.g.

$1+2+3+4\dots - (1+1+1+1\dots)=0+1+2+3+4\dots$

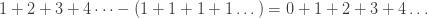
Now, let me define a new function

$\xi(s)=\zeta(s)-\zeta(s+1)$

$\xi(-1)$

is the sum over the natural numbers and by analytic continuation

$\xi(-1)=-1/12+1/2=5/12$

and thus the sum over the natural numbers is now 5/12. Again, if you try to do arithmetic with infinity, you can get almost anything. A fun exercise is to create some other examples.

Biology Magazine

Nonuniqueness of -1/12

About the author

Author's Latest Articles

Magazines

COMMUNITY BIOLOGY