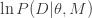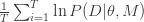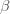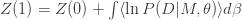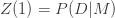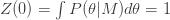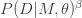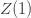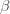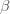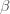In a previous post, I summarized the Bayesian approach to model comparison, which requires the calculation of the Bayes factor between two models. Here I will show one computational approach that I use called thermodynamic integration borrowed from molecular dynamics. Recall, that we need to compute the model likelihood function
(1)
for each model where
is just the parameter dependent likelihood function we used to find the posterior probabilities for the parameters of the model.
The integration over the parameters can be accomplished using the Markov Chain Monte Carlo, which I summarized previously here. We will start by defining the partition function
(2)
where
is an inverse temperature. The derivative of the log of the partition function gives
(3)
which is equal to the ensemble average of
. However, if we assume that the MCMC has reached stationarity then we can replace the ensemble average with a time average
. Integrating (3) over
from 0 to 1 gives
From (1) and (2), we see that
, which is what we want to compute and
.
Hence, to perform Bayesian model comparison, we simply run the MCMC for each model at different temperatures (i.e. use
as the likelihood in the standard MCMC) and then integrate the log likelihoods
over
at the end. For a Gaussian likelihood function, changing temperature is equivalent to changing the data “error”. The higher the temperature the larger the presumed error. In practice, I usually run at seven to ten different values of
and use a simple trapezoidal rule to integrate over
. I can even do parameter inference and model comparison in the same MCMC run.
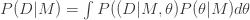
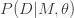
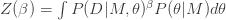
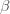
![\frac{d}{d\beta}\ln Z(\beta)=\frac{\int d\theta \ln[P(D |\theta,M)] P(D | \theta, M)^\beta P(\theta|M)}{\int d\theta \ P(D | \theta, M)^\beta P(\theta | M)}](http://m5.paperblog.com/i/52/525755/bayesian-model-comparison-part-2-L-9Siyl6.jpeg "\frac{d}{d\beta}\ln Z(\beta)=\frac{\int d\theta \ln[P(D |\theta,M)] P(D | \theta, M)^\beta P(\theta|M)}{\int d\theta \ P(D | \theta, M)^\beta P(\theta | M)}")
