What’s AI? – Part 2, on the Contrasting Natures of Symbolic and Statistical Semantics

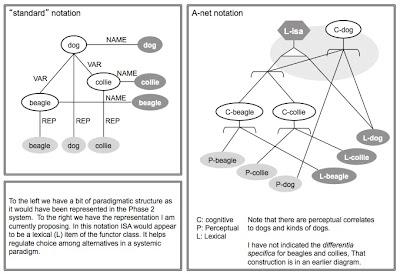
Comparison of Semantic Nets (left) with Attractor Nets (right). See below.

Color me pleased with the AI essay I just published in 3 Quarks Daily, Some Notes On Computers, AI, And The Mind, and my follow-up here, What’s AI? – @3QD [& the contrasting natures of symbolic and statistical semantics]. These notes are, in turn, a follow-up to my follow-up. In particular, I want to elaborate on these concluding paragraphs:

Now, let’s compare these two systems. In the symbolic computation semantics we have a relational graph where both the nodes and the arcs are labeled. All that matters is the topology of the graph, that is, the connectivity of the nodes and arcs, and the labels on the nodes and arcs. The nature of those labels is very important.
In the statistical system words are in fixed geometric positions in a high-dimensional space; exact positions, that is, distances, are critical. This system, however, doesn’t need node and arc labels. The vectors do all the work.

These statements are, I feel, at the right level of generalization and abstraction. The purpose of these notes is to lay out some of the things that would have to be taken into consideration in order to further develop those ideas.
HOWEVER, it’s sketchy & full of holes. First the sketchy stuff. Then I’ve got links to material that’s somewhat more worked out. It’ll help full in the holes and flesh out the details.
Stream of consciousness ramble-through

Caveat: These are informal notes, mostly for myself. I list them here as place-holders for work that needs to be done.

How do you make inference in the system? Symbolic model allows for a logic based on node and arc types. Such a model treats the knowledge structure as a database and makes inferences over it. Humans are not like that. In statistical systems there is no capacity for ‘externally’ guided inference. All inference is ‘black-boxed’ and internal to the system.
How do you add “meaning” to a statistical model? What is “meaning” anyhow? Does meaning ultimately require/imply interactive coupling with [living in] a world? And doesn’t it imply/require an intending subject?
Is this the ultimate import of critiques such as those of Dreyfus and Searle? But aren’t those ‘cheap’ critiques, arrived at without knowledge of how these systems work? And what of it?
How do we get rid of arc and node labels? Doesn’t that amount to coupling with the external world? See David Hays in Cognitive Structures (HRAF Press 1981) and Sydney Lamb’s notation for his stratificational grammar. And then we have my attractor nets, where the nodes are logical operators over attractor landscapes and the arcs are attractors within those landscapes.
If symbolic systems are more flexible and ‘deeper’ how come the statistical systems are more powerful in actual applications? The symbolic systems get their knowledge directly from the humans that design them. The makers decide on node and arc types and the way to make inferences over them; and the makers encode knowledge directly into the system. Statistical systems learn. NLP systems in effect back in to a simulacrum of the knowledge humans have ‘baked-in’ to the texts they generate. But what about visual systems based on unsupervised learning? Those systems are directly ‘in touch with’ an ‘external world’, no?
What about the phenomenal power of chess and Go programs? These programs are now more powerful than the best human players. I note as well that neither chess nor Go require contact with a rich physical world. Both take place in a 2D world containing a very limited universe of objects and in which there are very limited opportunities for action. For all practical purposes, there is no world external to the computer, unlike what we have for translation systems, text generation systems, or car-driving systems. Does this imply that perhaps the best and most powerful use of these systems is in the internal configuration of and maintenance of computational systems themselves? But won’t that make these systems even more ‘black-boxy’ than they already are?
And speech-to-text, text-to-speech?
Note that learning systems of various sorts do require exposure to mountains of data, whether externally generated and presented to the system or created by the system itself (as in game systems that compete against themselves). Humans do not require exposure to so many cases for effective learning. What’s this about? Well, for one thing it’s about having a brain and body that evolved to fit the world: no blank slate. Does is all cascade back on to that, or is there more?
Natural intelligence and metaphor
While much of my work with David Hays was anchored in a symbolic systems approach to the mind, we did venture elsewhere. Thus when the symbolic systems approach collapsed in the mid-1980s we were, if not exactly prepared, able to keep moving on. We had other conceptual irons in the forge.
In Cognitive Structures, which I linked above, Hays came up with a scheme to ground a digital cognitive system in an analog sensorimotor system. A few years after that he and I worked on a paper where we grounded our whole system in neural systems:

William L. Benzon and David G. Hays, Principles and development of natural intelligence, Journal of Social and Biological Systems 11, 293-322, 1988, https://www.academia.edu/235116/Principles_and_Development_of_Natural_Intelligence.
Abstract: The phenomena of natural intelligence can be grouped into five classes, and a specific principle of information processing, implemented in neural tissue, produces each class of phenomena. (1) The modal principle subserves feeling and is implemented in the reticular formation. (2) The diagonalization principle subserves coherence and is the basic principle, implemented in neocortex. (3) Action is subserved by the decision principle, which involves interlinked positive and negative feedback loops, and resides in modally differentiated cortex. (4) The problem of finitization resolves into a figural principle, implemented in secondary cortical areas; figurality resolves the conflict between pro-positional and Gestalt accounts of mental representations. (5) Finally, the phenomena of analysis reflect the action of the indexing principle, which is implemented through the neural mechanisms of language.
These principles have an intrinsic ordering (as given above) such that implementation of each principle presupposes the prior implementation of its predecessor. This ordering is preserved in phylogeny: (1) mode, vertebrates; (2) diagonalization, reptiles; (3) decision, mammals; (4) figural, primates; (5) indexing. Homo sapiens sapiens. The same ordering appears in human ontogeny and corresponds to Piaget's stages of intellectual development, and to stages of language acquisition.

I note that we conceived of the second principle, diagonalization, as involving holograph-like processing, which involves convolution. Convolution is important in some forms of contemporary neural net systems. Subsequently we published a paper in which we used convolution to account for metaphor:

William L. Benzon and David G. Hays, Metaphor, Recognition, and Neural Process, The American Journal of Semiotics, Vol. 5. No. 1 (1987), 59-80, https://www.academia.edu/238608/Metaphor_Recognition_and_Neural_Process.
Abstract: Karl Pribram's concept of neural holography suggests a neurological basis for metaphor: the brain creates a new concept by the metaphoric process of using one concept as a filter — better, as an extractor — for another. For example, the concept "Achilles" is "filtered" through the concept "lion" to foreground the pattern of fighting fury the two hold in common. In this model the linguistic capacity of the left cortical hemisphere is augmented by the capacity of the right hemisphere for analysis of images. Left-hemisphere syntax holds the tenor and vehicle in place while right-hemisphere imaging process extracts the metaphor ground. Metaphors can be concatenated one after the other so that the ground of one metaphor can enter into another one as tenor or vehicle. Thus conceived metaphor is a mechanism through which thought can be extended into new conceptual territory.

Attractor Nets
In my book on the brain, Beethoven’s Anvil (2001), I’d drawn on Walter Freeman’s neurodynamics for some fundamental concepts. I’ve placed final chapter drafts of some of that work online:

Brains, Music and Coupling, https://www.academia.edu/232642/Beethovens_Anvil_Music_in_Mind_and_Culture.

A couple years later I began exploring the possibility of using Sydney Lamb’s relational network approach for linguistics to represent the logical structure of complex attractor landscapes – an attractor net. If we’re going to think about human cognition in terms of the complex dynamics of the brain, considered as a neural net having a phase space of very high dimensionality, we’re going to need a way of thinking about processes in a topology of thousands of attractors related to one another in complex ways. I think Lamb’s notation may be a way of representing the topology of such an attractor landscape.
As is typically the case in such matters, we’ve got multiple levels of modeling/representation. In this case, two. The bottom level is the standard world of complex dynamics with its systems of equations which are used to analyze and build computer simulations of neural nets and to analyze neural and behavioral data. I have nothing to say about the details of this level. I’m interested in the upper level, where we’re trying to represent the relationship between the large number of attractors in a rich neural network. We can’t think about this structure by examining the underlying system of equations, nor even by examining such computer simulations as we are currently capable of running.
I am imagining, in the large, that we have a neural net where we can make meaningful distinctions between microscopic, mesoscopic, and macroscopic processes. Roughly speaking, I see Lamb’s notation as a way to begin thinking about the relationship between mesoscopic and macroscopic processes.
These notes are of a preliminary and very informal nature. I’m just trying things out to see what’s involved in doing this.

Attractor Nets, Series I: Notes Toward a New Theory of Mind, Logic and Dynamics in Relational Networks (2011) 52 pp. https://www.academia.edu/9012847/Attractor_Nets_Series_I_Notes_Toward_a_New_Theory_of_Mind_Logic_and_Dynamics_in_Relational_Networks.
Attractor Nets 2011: Diagrams for a New Theory of Mind (2011) 55 pp. https://www.academia.edu/9012810/Attractor_Nets_2011_Diagrams_for_a_New_Theory_of_Mind.

Fluid Mind
More notes, semi-organized, with references:

William Benzon, From Associative Nets to the Fluid Mind (2013), https://www.academia.edu/9508938/From_Associative_Nets_to_the_Fluid_Mind.
Framing: We can think of the mind as a network that’s fluid on several scales of viscosity. Some things change very slowly, on a scale of months to years. Other things change rapidly, in milliseconds or seconds. And other processes are in between. The microscale dynamic properties of the mind at any time are context dependent. Under some conditions it will function as a highly structured cognitive network; the details of the network will of course depend on the exact conditions, both internal (including chemical) and external (what’s the “load” on the mind?). Under other conditions the mind will function more like a loose associative net. These notes explore these notions in a very informal way.
Contents
Fluid Nets – Or, the Mind is Not the Brain 1

The Mind is a Fixed Cognitive Network 1
The Mind as Neural Weather 2
Fluid Nets and a Poet’s Mind 3
Some References 5

Associative Nets 6

1. Introduction 6
2. Definitions 6
3. Why An Associative Net?: “US History” As A Gestalt 7
4. What Does This Get Us? 9
5. Reception Vs. Production Vocabulary 10
6. Antonyms And Other Associations 10
7. The “Real” Abstraction 11
8. Relations Between Clusters 12
9. Desire And Emotion 12
10. Two Forms Of Representation & Their Interaction 12
11. The Neural Basis 14
12. On The Overall Scheme Of Things 14
Some Associative Clusters 15